
分析 (Ⅰ)去掉绝对值得到关于x的不等式组,解出即可;
(Ⅱ)求出a+b+c=2,根据基本不等式的性质,求出代数式的最小值.
解答 解:(Ⅰ)由题意得:
$\left\{\begin{array}{l}x<-1\\ x-3≥x-1\end{array}\right.$,或$\left\{\begin{array}{l}-1≤x≤1\\ 3x-1≥x-1\end{array}\right.$,或$\left\{\begin{array}{l}x>1\\-x+3≥x-1\end{array}\right.$,
解得:0≤x≤2,
故不等式的解集为[0,2];
(Ⅱ)$f(x)=\left\{\begin{array}{l}x-3,x<-1\\ 3x-1,-1≤x≤1\\-x+3,x>1\end{array}\right.$,
显然当x=1时,f(x)有大值,m=f(1)=2,
∴a+b+c=2,
而$({a+b+c})({\frac{b^2}{a}+\frac{c^2}{b}+\frac{a^2}{c}})=[{{{({\sqrt{a}})}^2}+{{({\sqrt{b}})}^2}+{{({\sqrt{c}})}^2}}][{{{({\frac{b}{{\sqrt{a}}}})}^2}+{{({\frac{c}{{\sqrt{b}}}})}^2}+{{({\frac{a}{{\sqrt{c}}}})}^2}}]≥{({a+b+c})^2}$,
∴$\frac{b^2}{a}+\frac{c^2}{b}+\frac{a^2}{c}≥a+b+c=2$,
当且仅当$\left\{\begin{array}{l}\frac{{\sqrt{a}}}{{\frac{b}{{\sqrt{a}}}}}=\frac{{\sqrt{b}}}{{\frac{c}{{\sqrt{b}}}}}=\frac{{\sqrt{c}}}{{\frac{a}{{\sqrt{c}}}}}\\ a+b+c=2\end{array}\right.$,即$a=b=c=\frac{2}{3}$时取等号,
故$\frac{b^2}{a}+\frac{c^2}{b}+\frac{a^2}{c}$的最小值是2.
点评 本题考查了绝对值不等式的性质,考查基本不等式的性质,是一道中档题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源:2017届湖北省百所重点校高三联合考试数学(理)试卷(解析版) 题型:选择题
已知命题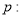 对任意
对任意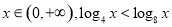 ,命题
,命题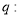 存在
存在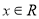 ,使得
,使得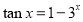 ,则下列命题为真命题的是( )
,则下列命题为真命题的是( )
A.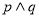 B.
B.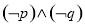 C.
C.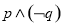 D.
D.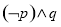
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 平均车速超过80km/h | 平均车速不超过80km/h | 合计 | |
| 男性驾驶员 | |||
| 女性驾驶员 | |||
| 合计 |
| P(K2≥k) | 0.1500 | 0.1000 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com