
分析 将函数化为y=Asin(ωx+φ)的形式,将内层函数放到正弦函数的增区间上,解不等式得函数的单调递增区间;x∈[0,2π),k取不同的值,可得在x∈[0,π]的单调递增区间.
(2)当-2<f(x)-m<2,在x∈[$\frac{π}{6}$,$\frac{2π}{3}$]时,转化求f(x)+2的最小值,求f(x)-2的值最大值,即可求实数m的取值范围.
解答 解:函数f(x)=4sinx•sin2(${\frac{π+2x}{4}}$)-sin2x+cos2x.
化简:f(x)=4sinx•$\frac{1-cos(\frac{π}{2}+x)}{2}$-sin2x+cos2x.
=2sinx(1+sinx)-sin2x+cos2x.
=2sinx+2sin2x-sin2x+cos2x.
=2sinx+1,
∵x∈[0,2π)
由正弦函数的性质可知:x∈[$2kπ-\frac{π}{2}$,$2kπ+\frac{π}{2}$]是单调递增区间,
∴当k=0时,可得[0,$\frac{π}{2}$]是单调递增区间,
当k=1时,可得[$\frac{3π}{2}$,2π]是单调递增区间,
故得f(x)在x∈[0,2π)上的增区间是[0,$\frac{π}{2}$]和[$\frac{3π}{2}$,2π).
(2)由(1)可知f(x)=2sinx+1
∵A⊆B
∴则x∈[$\frac{π}{6}$,$\frac{2π}{3}$]时,使-2<f(x)-m<2恒成立,转化为:f(x)-2<m<2+f(x)恒成立;
等价于:[f(x)-2]max<m<[2+f(x)]min
当x=$\frac{π}{6}$时,f(x)取得最小值为2.
当x=$\frac{π}{2}$时,f(x)取得最大值为3.
∴[f(x)-2]max=1,[2+f(x)]min=4
故得:1<m<4
所以实数m的取值范围(1,4).
点评 本题考查了三角函数的化简能力以及三角函数性质的运用解决恒成立问题.属于中档题.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 椭圆 | B. | 双曲线 | C. | 线段 | D. | 两条射线 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | -10 | C. | 5 | D. | -15 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
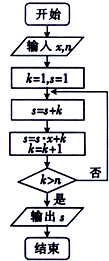 执行如图所示的程序框图.
执行如图所示的程序框图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com