
分析 原不等式化为(x-a-1)(x+2a-3)<0,由x=0是不等式的解,得(a+1)(2a-3)>0,求出a的取值范围;再讨论a的取值,写出原不等式的解集.
解答 解:原不等式可化为(x-a-1)(x+2a-3)<0,(1分)
由x=0适合不等式得(a+1)(2a-3)>0,(3分)
所以a<-1或a>$\frac{3}{2}$;(4分)
若a<-1,则3-2a>a+1,
此时不等式的解集是(a+1,3-2a);(6分)
若a>$\frac{3}{2}$,由-2a+3-(a+1)=-3a+2<0,所以3-2a<a+1,
此时不等式的解集是(3-2a,a+1);(9分)
综上,当a<-1时,M为(a+1,3-2a),
当a>$\frac{3}{2}$时,M为(3-2a,a+1).(10分)
点评 本题考查了含有字母系数的一元二次不等式的解法与应用问题,是综合题.


科目:高中数学 来源: 题型:选择题
| A. | [$\frac{\sqrt{3}}{3}$,$\frac{2\sqrt{2}}{3}$] | B. | [$\frac{\sqrt{6}}{3}$,$\frac{2\sqrt{2}}{3}$] | C. | [$\frac{2\sqrt{2}}{3}$,1] | D. | [$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{6}}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|2≤x≤3} | B. | {x|-2≤x≤3} | C. | {x|-2≤x<2} | D. | {x|-4<x≤3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (-∞,1] | C. | (1,+∞) | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
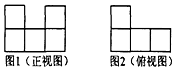 用若干个棱长为1cm的小正方体叠成一个几何体,图1为其正视图,图2为其俯视图,若这个几何体的体积为7cm3,则其侧视图为( )
用若干个棱长为1cm的小正方体叠成一个几何体,图1为其正视图,图2为其俯视图,若这个几何体的体积为7cm3,则其侧视图为( )| A. | 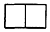 | B. | 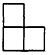 | C. |  | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com