
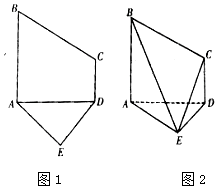
 已知五边形ABCDE是由直角梯形ABCD和等腰直角三角形ADE构成,如图所示,AB⊥AD,AE⊥DE,AB∥CD,且AB=2CD=2DE=4,将五边形ABCDE沿着AD折起,且使平面ABCD⊥平面ADE.
已知五边形ABCDE是由直角梯形ABCD和等腰直角三角形ADE构成,如图所示,AB⊥AD,AE⊥DE,AB∥CD,且AB=2CD=2DE=4,将五边形ABCDE沿着AD折起,且使平面ABCD⊥平面ADE.分析 (Ⅰ)取BC中点为N,AD中点为P,连接MN,NP,MP.推导出MP∥面ABE,NP∥面ABE,由此能求出边AB上存在一点N,使得MN∥平面ABE,且$\frac{BN}{BC}=\frac{1}{2}$.
(Ⅱ)推导出EP⊥AD,由四面体B-CDE的体积VB-CDE=VE-BCD,能求出结果.
解答 解:(Ⅰ)取BC中点为N,AD中点为P,连接MN,NP,MP.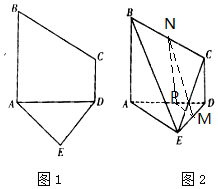
∵MP∥AE,AE⊆面ABE,MP?面ABE,
∴MP∥面ABE,同理NP∥面ABE,
又MP∩NP=P,∴MN∥面ABE,
∴边AB上存在一点N,使得MN∥平面ABE,且$\frac{BN}{BC}=\frac{1}{2}$.
(Ⅱ)∵△ADE为等腰直角三角形.
∴EP⊥AD,
又平面ABCD平面ADE,∴EP⊥平面ABCD,
∵$EP=\sqrt{2}$,${S_{△BCD}}=2\sqrt{2}$,
∴四面体B-CDE的体积VB-CDE=VE-BCD=$\frac{1}{3}×EP×{S_{△BCD}}$=$\frac{1}{3}×\sqrt{2}×2\sqrt{2}=\frac{4}{3}$.
点评 本题考查几何体的体积及直线与直线、直线与平面、平面与平面的位置关系等基础知识,考查考查推理论证能力、运算求解能力、空间想象能力,考查化归转化思想,数形结合思想,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | $({\frac{9}{4},+∞})$ | B. | $({\frac{3}{2},+∞})$ | C. | $({\sqrt{2},+∞})$ | D. | (3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{m-1}{m+1}$ | B. | $\frac{m}{m+1}$ | C. | $\frac{m-1}{m}$ | D. | $\frac{{2\sqrt{m}}}{m+1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $2\sqrt{3}$ | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 平均每天锻炼 的时间(分钟) | [0,10) | [10,20) | [20,30) | [30,40) | [40,50) | [50,60) |
| 总人数 | 20 | 36 | 44 | 50 | 40 | 10 |
| 课外体育不达标 | 课外体育达标 | 合计 | |
| 男 | |||
| 女 | 20 | 110 | |
| 合计 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 | … |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com