
| A. | $({\frac{9}{4},+∞})$ | B. | $({\frac{3}{2},+∞})$ | C. | $({\sqrt{2},+∞})$ | D. | (3,+∞) |
分析 由f(x)>xf'(x)成立,可得[$\frac{f(x)}{x}$]′<0,设g(x)=$\frac{f(x)}{x}$=lnx+(x-a)2,
则存在$x∈[{\frac{1}{2},2}]$,使得g′(x)=$\frac{1}{x}$+2(x-a)<0成立,a>(x+$\frac{1}{2x}$)min.
解答 解:由f(x)>xf'(x)成立,可得[$\frac{f(x)}{x}$′<0,设g(x)=$\frac{f(x)}{x}$=lnx+(x-a)2,
则存在$x∈[{\frac{1}{2},2}]$,使得g′(x)<0成立,即g′(x)=$\frac{1}{x}$+2(x-a)<0成立,即a>x+$\frac{1}{2x}$成立.
a>(x+$\frac{1}{2x}$)min.又x+$\frac{1}{2x}$≥2$\sqrt{x•\frac{1}{2x}}$=$\sqrt{2}$,∴$a>\sqrt{2}$.当且仅当x=$\frac{\sqrt{2}}{2}$时取等号.
故选:C
点评 本题考查了导数的应用,分离参数法求参数范围,属于中档题.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{\frac{5}{6},+∞})$ | B. | [2,+∞) | C. | $[{\frac{10}{3},+∞})$ | D. | [10,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
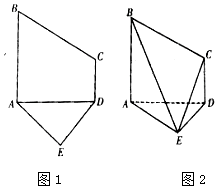 已知五边形ABCDE是由直角梯形ABCD和等腰直角三角形ADE构成,如图所示,AB⊥AD,AE⊥DE,AB∥CD,且AB=2CD=2DE=4,将五边形ABCDE沿着AD折起,且使平面ABCD⊥平面ADE.
已知五边形ABCDE是由直角梯形ABCD和等腰直角三角形ADE构成,如图所示,AB⊥AD,AE⊥DE,AB∥CD,且AB=2CD=2DE=4,将五边形ABCDE沿着AD折起,且使平面ABCD⊥平面ADE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com