
分析 利用点到直线的距离公式求出满足条件的点的弧长、几何概型的计算公式即可得出.
解答 解:由点到直线的距离公式得点O到直线x+y=1的距离为$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
故到直线x+y=1距离为$\frac{\sqrt{2}}{2}$的点在直线x+y=0和x+y+2=0上,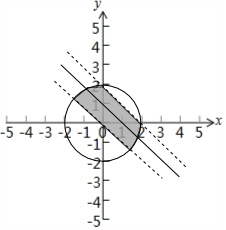
满足P到直线x+y=1的距离小于$\frac{\sqrt{2}}{2}$的点位于两直线之间的弧上,且两段弧度和为90°.
故概率P=$\frac{\frac{1}{4}×4π+\frac{1}{2}×2×2}{4π}$=$\frac{π+2}{4π}$.
故答案为:$\frac{π+2}{4π}$
点评 熟练掌握点到直线的距离公式及几何概型的计算公式是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
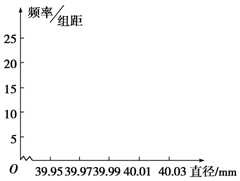 某制造商为运动会生产一批直径为40mm的乒乓球,现随机抽样检查20只,测得每只球的直径(单位:mm,保留两位小数)如下:
某制造商为运动会生产一批直径为40mm的乒乓球,现随机抽样检查20只,测得每只球的直径(单位:mm,保留两位小数)如下:| 40.02 | 40.00 | 39.98 | 40.00 | 39.99 |
| 40.00 | 39.98 | 40.01 | 39.98 | 39.99 |
| 40.00 | 39.99 | 39.95 | 40.01 | 40.02 |
| 39.98 | 40.00 | 39.99 | 40.00 | 39.96 |
| 分组 | 频数 | 频率 | $\frac{频率}{组距}$ |
| [39.95,39.97) | 2 | ||
| [39.97,39.99) | 4 | ||
| [39.99,40.01) | 10 | ||
| [40.01,40.03] | 4 | ||
| 合计 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
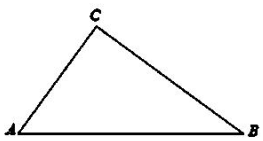 如图,A,B,C三地有直道相通,AB=10 千米,AC=6 千米,BC=8千米.现甲、乙两人同时从A地出发匀速前往B地,经过t小时,他们之间的距离为f(t)(单位:千米).甲的路线是AB,速度为10千米/小时,乙的路线是ACB,速度为16千米/小时.乙到达B地后原地等待.设t=t1时乙到达C地.
如图,A,B,C三地有直道相通,AB=10 千米,AC=6 千米,BC=8千米.现甲、乙两人同时从A地出发匀速前往B地,经过t小时,他们之间的距离为f(t)(单位:千米).甲的路线是AB,速度为10千米/小时,乙的路线是ACB,速度为16千米/小时.乙到达B地后原地等待.设t=t1时乙到达C地.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=x2+2x|x-a|,其中a∈R.
已知函数f(x)=x2+2x|x-a|,其中a∈R.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com