
【题目】甲、乙两人玩转盘游戏,该游戏规则是这样的:一个质地均匀的标有12等分数字格的转盘(如图),甲、乙两人各转转盘一次,转盘停止时指针所指的数字为该人的得分.(假设指针不能指向分界线)现甲先转,乙后转,求下列事件发生的概率 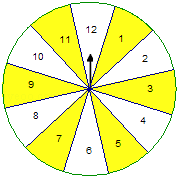
(1)甲得分超过7分的概率.
(2)甲得7分,且乙得10分的概率
(3)甲得5分且获胜的概率.
【答案】
(1)解:甲先转,甲得分超过(7分)为事件A,
记事件A1:甲得(8分),记事件A2:甲得(9分),
记事件A3:甲得(10分),记事件A4:甲得(11分),
记事件A5:甲得(12分),
由几何概型求法,以上事件发生的概率均为 ![]() ,
,
甲得分超过(7分)为事件A,A=A1∪A2∪A3∪A4∪A5
P(A)=P(A1∪A2∪A3∪A4∪A5)= ![]()
(2)解:记事件C:甲得(7分)并且乙得(10分),
以甲得分为x,乙得分为y,组成有序实数对(x,y),可以发现,x=1的数对有12个,同样x等于2,3,4,5,6,7,8,9,10,11,12的数对也有12个,所以这样的有序实数对(x,y)有144个,
其中甲得(7分),乙得(10分)为(7,10)共1个,P(C)= ![]()
(3)解:甲先转,得(5分),且甲获胜的基本事件为(5,4)(5,3)(5,2)(5,1)
则甲获胜的概率P(D)= ![]()
【解析】(1)甲先转,甲得分超过(7分)为事件A,记事件A1:甲得(8分),记事件A2:甲得(9分),记事件A3:甲得(10分),记事件A4:甲得(11分),记事件A5:甲得(12分),由几何概型求法,即可求得甲得分超过7分的概率.(2)记事件C:甲得(7分)并且乙得(10分),以甲得分为x,乙得分为y,组成有序实数对(x,y),可以发现,x=1的数对有12个,同样x等于2,3,4,5,6,7,8,9,10,11,12的数对也有12个,所以由古典概型求法,即可求得甲得分超过7分的概率;(3)甲先转,得(5分),且甲获胜的基本事件为(5,4)(5,3)(5,2)(5,1)由古典概型求法,即可求得甲获胜的概率.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:
【题目】如图是某社区工会对当地企业工人月收入情况进行一次抽样调查后画出的频率分布直方图,其中第二组月收入在[1.5,2)千元的频数为300,则此次抽样的样本容量为( ) 
A.1000
B.2000
C.3000
D.4000
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一次测验共有4个选择题和2个填空题,每答对一个选择题得20分,每答对一个填空题得10分,答错或不答得0分,若某同学答对每个选择题的概率均为 ![]() ,答对每个填空题的概率均为
,答对每个填空题的概率均为 ![]() ,且每个题答对与否互不影响.
,且每个题答对与否互不影响.
(1)求该同学得80分的概率;
(2)若该同学已经答对了3个选择题和1个填空题,记他这次测验的得分为ξ,求ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某印刷厂为了研究印刷单册书籍的成本y(单位:元)与印刷册数x(单位:千册)之间的关系,在印制某种书籍时进行了统计,相关数据见下表:

根据以上数据,技术人员分别借助甲、乙两种不同的回归模型,得到了两个回归方程,甲: ![]()
为了评价两种模型的拟合效果,完成以下任务:
(1)(ⅰ)完成下表(计算结果精确到0.1):

(ⅱ)分别计算模型甲与模型乙的残差平方和![]() 及
及![]() ,并通过比较
,并通过比较![]() ,
,![]() 的大小,判断哪个模型拟合效果更好.
的大小,判断哪个模型拟合效果更好.
(2)该书上市后,受到广大读者的热烈欢迎,不久便全部售罄,于是印刷厂决定进行二次印刷,根据市场调查,新需求量为8千册(概率为0.8)或10千册(概率为0.2),若印刷厂以没测5元的价格将书籍出售给订货商,问印刷厂二次印刷8千册还是10千册恒获得更多的利润?(按(1)中拟合效果较好的模型计算印刷单册书的成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知空间四边形ABCD的两条对角线的长AC=6,BD=8,AC与BD所成的角为30o , E,F,G,H分别是AB,BC,CD,DA的中点,求四边形EFGH的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCED中,PD⊥面ABCD,四边形ABCD为平行四边形,∠DAB=60°,AB=PA=2AD=4, 
(1)若E为PC中点,求证:PA∥平面BDE
(2)求三棱锥D﹣BCP的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 过点
过点![]() ,
, ![]() 为椭圆的半焦距,且
为椭圆的半焦距,且![]() ,过点
,过点![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() ,
, ![]() 与椭圆
与椭圆![]() 分别交于另两点
分别交于另两点![]() ,
, ![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 的斜率为
的斜率为![]() ,求
,求![]() 的面积;
的面积;
(3)若线段![]() 的中点在
的中点在![]() 轴上,求直线
轴上,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设p:实数x满足x2﹣4ax+3a2<0,其中a>0,命题q:实数x满足 ![]() .
.
(1)若a=1,且p∨q为真,求实数x的取值范围;
(2)若p是q的必要不充分要条件,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com