
°ĺŐ‚ńŅ°Ņń≥”°ňĘ≥ßő™Ńň—–ĺŅ”°ňĘĶ•≤Š ťľģĶń≥…Īĺy£®Ķ•őĽ£ļ‘™£©”Ž”°ňĘ≤Š żx£®Ķ•őĽ£ļ«ß≤Š£©÷ģľšĶńĻōŌĶ£¨‘ŕ”°÷∆ń≥÷÷ ťľģ ĪĹÝ––ŃňÕ≥ľ∆£¨ŌŗĻō żĺ›ľŻŌ¬ĪŪ£ļ

łý囓‘…Ō żĺ›£¨ľľ ű»ň‘Ī∑÷ĪūĹŤ÷ķľ◊°Ę““ŃĹ÷÷≤ĽÕ¨ĶńĽōĻťń£–Õ£¨Ķ√ĶĹŃňŃĹłŲĽōĻť∑Ĺ≥Ő£¨ľ◊£ļ ![]()
ő™Ńň∆ņľŘŃĹ÷÷ń£–ÕĶńń‚ļŌ–ßĻŻ£¨ÕÍ≥…“‘Ō¬»őőŮ£ļ
£®1£©£®Ę°£©ÕÍ≥…Ō¬ĪŪ£®ľ∆ň„ĹŠĻŻĺę»∑ĶĹ0.1£©£ļ

£®ĘĘ£©∑÷Īūľ∆ň„ń£–Õľ◊”Žń£–Õ““Ķń≤–≤Ó∆Ĺ∑ĹļÕ![]() ľį
ľį![]() £¨≤ĘÕ®ĻżĪ»ĹŌ
£¨≤ĘÕ®ĻżĪ»ĹŌ![]() ,
,![]() Ķńīů–°£¨Ň–∂ŌńńłŲń£–Õń‚ļŌ–ßĻŻłŁļ√.
Ķńīů–°£¨Ň–∂ŌńńłŲń£–Õń‚ļŌ–ßĻŻłŁļ√.
£®2£©ł√ ť…Ō –ļů£¨ ‹ĶĹĻ„īů∂Ń’ŖĶń»»Ń“Ľ∂”≠£¨≤Ľĺ√Ī„»ę≤Ņ Řůņ£¨”ŕ «”°ňĘ≥ßĺŲ∂®ĹÝ––∂Ģīő”°ňĘ£¨łýĺ› –≥°Ķų≤ť£¨–¬–Ť«ůŃŅő™8«ß≤Š£®łŇ¬ ő™0.8£©ĽÚ10«ß≤Š£®łŇ¬ ő™0.2£©£¨»Ű”°ňĘ≥ß“‘√Ľ≤‚5‘™ĶńľŘłŮĹę ťľģ≥Ų ŘłÝ∂©Ľű…Ő£¨ő ”°ňĘ≥ß∂Ģīő”°ňĘ8«ß≤ŠĽĻ «10«ß≤Šļ„ĽŮĶ√łŁ∂ŗĶńņŻ»ů£Ņ£®įī£®1£©÷–ń‚ļŌ–ßĻŻĹŌļ√Ķńń£–Õľ∆ň„”°ňĘĶ•≤Š ťĶń≥…Īĺ£©
°ĺīūįł°Ņ£®1£©(Ę°)ľŻĹ‚őŲ(ĘĘ)ń£–Õ““Ķńń‚ļŌ–ßĻŻłŁļ√£ģ£®2£©”°ňĘ8«ß≤Š∂‘”°ňĘ≥ßłŁ”–ņŻ£ģ
°ĺĹ‚őŲ°Ņ ‘Ő‚∑÷őŲ£ļ£®1£©(Ę°)łýĺ›Ļę Ĺľ∆ň„£¨ŐÓ»Ž∂‘”¶ĪŪłŮ(ĘĘ) Ī»ĹŌ≤–≤Ó∆Ĺ∑ĹļÕīů–°£¨‘Ĺ–°‘Ĺļ√£¨Ļ ń£–Õ““Ķńń‚ļŌ–ßĻŻłŁļ√£ģ£®2£©∑÷Īūľ∆ň„”°ňĘ8«ß≤Š”Ž10«ß≤ŠĶńņŻ»ů£ļ∂Ģīő”°ňĘ8«ß≤Š£¨‘Ú”°ňĘ≥߼ŮņŻő™![]() (‘™)£¨»Á∂Ģīő”°ňĘ10«ß≤Š£¨‘Ú√Ņ≤Š≥…Īĺő™
(‘™)£¨»Á∂Ģīő”°ňĘ10«ß≤Š£¨‘Ú√Ņ≤Š≥…Īĺő™![]() £¨–Ť«ů∆ŕÕŻ÷Ķő™
£¨–Ť«ů∆ŕÕŻ÷Ķő™![]() £ģ“Ú∂ÝĽŮņŻő™
£ģ“Ú∂ÝĽŮņŻő™![]() £¨…Ŕ”ŕ”°ňĘ8«ß≤ŠĽŮĶńņŻ»ů.
£¨…Ŕ”ŕ”°ňĘ8«ß≤ŠĽŮĶńņŻ»ů.
‘Ő‚Ĺ‚őŲ£ļĹ‚£ļ(ĘŮ) (Ę°) ĺ≠ľ∆ň„£¨Ņ…Ķ√Ō¬ĪŪ£ģ
”°ňĘ≤Š ż | 2 | 3 | 4 | 5 | 8 | |
Ķ•≤Š≥…Īĺ | 3.2 | 2.4 | 2 | 1.9 | 1.7 | |
ń£–Õľ◊ | Ļņľ∆÷Ķ | 3.1 | 2.4 | 2.1 | 1.9 | 1.6 |
≤–≤Ó | 0.1 | 0 | -0.1 | 0 | 0.1 | |
ń£–Õ““ | Ļņľ∆÷Ķ | 3.2 | 2.3 | 2 | 1.9 | 1.7 |
≤–≤Ó | 0 | 0.1 | 0 | 0 | 0 | |
(ĘĘ) ![]() £¨
£¨ ![]() £¨
£¨
![]() £¨Ļ ń£–Õ““Ķńń‚ļŌ–ßĻŻłŁļ√£ģ
£¨Ļ ń£–Õ““Ķńń‚ļŌ–ßĻŻłŁļ√£ģ
(ĘÚ) »Ű∂Ģīő”°ňĘ8«ß≤Š£¨‘Ú”°ňĘ≥߼ŮņŻő™![]() (‘™) £ģ
(‘™) £ģ
»Ű∂Ģīő”°ňĘ10«ß≤Š£¨”…(ĘŮ)Ņ…÷™£¨Ķ•≤Š ť”°ňĘ≥…Īĺő™![]() (‘™)£¨
(‘™)£¨
Ļ ”°ňĘ◊‹≥…Īĺő™![]() (‘™) £ģ
(‘™) £ģ
…Ť–¬–Ť«ůŃŅő™![]() («ß≤Š)£¨”°ňĘ≥ßņŻ»ůő™
(«ß≤Š)£¨”°ňĘ≥ßņŻ»ůő™![]() (‘™)£¨‘Ú
(‘™)£¨‘Ú
| 8 | 10 |
| 0.8 | 0.2 |
![]() £ģ
£ģ
Ļ ![]() £ģ
£ģ
Ļ ”°ňĘ8«ß≤Š∂‘”°ňĘ≥ßłŁ”–ņŻ£ģ



| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™‘≤CĶń∑Ĺ≥Őő™£ļx2+y2©Ā2mx©Ā2y+4m©Ā4=0£¨£®m° R£©£ģ
£®1£© ‘«ůmĶń÷Ķ£¨ Ļ‘≤CĶń√śĽż◊Ó–°£Ľ
£®2£©«ů”Ž¬ķ◊„£®1£©÷–ŐűľĢĶń‘≤CŌŗ«–£¨«“ĻżĶ„£®1£¨©Ā2£©Ķń÷ĪŌŖ∑Ĺ≥Ő£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™÷ĪŌŖ![]() Ķń≤ő ż∑Ĺ≥Őő™
Ķń≤ő ż∑Ĺ≥Őő™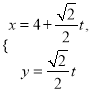 £®
£®![]() ő™≤ő ż£©£¨“‘◊ÝĪÍ‘≠Ķ„ő™ľęĶ„£¨
ő™≤ő ż£©£¨“‘◊ÝĪÍ‘≠Ķ„ő™ľęĶ„£¨ ![]() ÷ŠĶń∑«łļįŽ÷Šő™ľę÷ŠĹ®ŃĘľę◊ÝĪÍŌĶ£¨‘≤
÷ŠĶń∑«łļįŽ÷Šő™ľę÷ŠĹ®ŃĘľę◊ÝĪÍŌĶ£¨‘≤![]() Ķńľę◊ÝĪÍ∑Ĺ≥Őő™
Ķńľę◊ÝĪÍ∑Ĺ≥Őő™![]() £¨÷ĪŌŖ
£¨÷ĪŌŖ![]() ”Ž‘≤
”Ž‘≤![]() ĹĽ”ŕ
ĹĽ”ŕ![]() £¨
£¨ ![]() ŃĹĶ„.
ŃĹĶ„.
£®1£©«ů‘≤![]() Ķń÷ĪĹ«◊ÝĪÍ∑Ĺ≥ŐľįŌ“
Ķń÷ĪĹ«◊ÝĪÍ∑Ĺ≥ŐľįŌ“![]() Ķń≥§£Ľ
Ķń≥§£Ľ
£®2£©∂ĮĶ„![]() ‘ŕ‘≤
‘ŕ‘≤![]() …Ō£®≤Ľ”Ž
…Ō£®≤Ľ”Ž![]() £¨
£¨ ![]() ÷ōļŌ£©£¨ ‘«ů
÷ōļŌ£©£¨ ‘«ů![]() Ķń√śĽżĶń◊Óīů÷Ķ.
Ķń√śĽżĶń◊Óīů÷Ķ.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™ĺ≠Ōķń≥÷÷…Ő∆∑ĶńĶÁ…Ő‘ŕ»őļő“ĽłŲŌķ Řľĺ∂»ńŕ£¨√Ņ Ř≥Ų![]() ∂÷ł√…Ő∆∑Ņ…ĽŮņŻ»ů
∂÷ł√…Ő∆∑Ņ…ĽŮņŻ»ů![]() ÕÚ‘™£¨őī Ř≥ŲĶń…Ő∆∑£¨√Ņ
ÕÚ‘™£¨őī Ř≥ŲĶń…Ő∆∑£¨√Ņ![]() ∂÷Ņųňū
∂÷Ņųňū![]() ÕÚ‘™£ģłýĺ›ÕýńÍĶńŌķ Řĺ≠—ť£¨Ķ√ĶĹ“ĽłŲŌķ Řľĺ∂»ńŕ –≥°–Ť«ůŃŅĶń∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľ»Á”“Õľňý ĺ£ģ“—÷™ĶÁ…Őő™Ō¬“ĽłŲŌķ Řľĺ∂»≥ÔĪłŃň
ÕÚ‘™£ģłýĺ›ÕýńÍĶńŌķ Řĺ≠—ť£¨Ķ√ĶĹ“ĽłŲŌķ Řľĺ∂»ńŕ –≥°–Ť«ůŃŅĶń∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľ»Á”“Õľňý ĺ£ģ“—÷™ĶÁ…Őő™Ō¬“ĽłŲŌķ Řľĺ∂»≥ÔĪłŃň![]() ∂÷ł√…Ő∆∑£ģŌ÷“‘
∂÷ł√…Ő∆∑£ģŌ÷“‘![]() £®Ķ•őĽ£ļ∂÷£¨
£®Ķ•őĽ£ļ∂÷£¨ ![]() £©ĪŪ ĺŌ¬“ĽłŲŌķ Řľĺ∂»Ķń –≥°–Ť«ůŃŅ£¨
£©ĪŪ ĺŌ¬“ĽłŲŌķ Řľĺ∂»Ķń –≥°–Ť«ůŃŅ£¨ ![]() £®Ķ•őĽ£ļÕÚ‘™£©ĪŪ ĺł√ĶÁ…ŐŌ¬“ĽłŲŌķ Řľĺ∂»ńŕĺ≠Ōķł√…Ő∆∑ĽŮĶ√ĶńņŻ»ů£ģ
£®Ķ•őĽ£ļÕÚ‘™£©ĪŪ ĺł√ĶÁ…ŐŌ¬“ĽłŲŌķ Řľĺ∂»ńŕĺ≠Ōķł√…Ő∆∑ĽŮĶ√ĶńņŻ»ů£ģ
£®ĘŮ£©łýĺ›∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľ£¨Ļņľ∆“ĽłŲŌķ Řľĺ∂»ńŕ –≥°–Ť«ůŃŅ![]() Ķń∆Ĺĺý ż”Ž÷–őĽ żĶńīů–°£Ľ
Ķń∆Ĺĺý ż”Ž÷–őĽ żĶńīů–°£Ľ
£®ĘÚ£©łýĺ›÷Ī∑ĹÕľĻņľ∆ņŻ»ů![]() ≤Ľ…Ŕ”ŕ57ÕÚ‘™ĶńłŇ¬ .
≤Ľ…Ŕ”ŕ57ÕÚ‘™ĶńłŇ¬ .

≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™Ň◊őÔŌŖ![]() ĶńĹĻĶ„ő™
ĶńĹĻĶ„ő™![]() £¨÷ĪŌŖ
£¨÷ĪŌŖ![]() ”ŽŇ◊őÔŌŖ
”ŽŇ◊őÔŌŖ![]() ĹĽ”ŕ
ĹĽ”ŕ![]() ŃĹĶ„£ģ
ŃĹĶ„£ģ
£®ĘŮ£©»Ű÷ĪŌŖ![]() ĻżĹĻĶ„
ĻżĹĻĶ„![]() £¨«“”Ž‘≤
£¨«“”Ž‘≤![]() ĹĽ”ŕ
ĹĽ”ŕ![]() £®∆š÷–
£®∆š÷–![]() ‘ŕ
‘ŕ![]() ÷ŠÕ¨≤ŗ£©£¨«ů÷§£ļ
÷ŠÕ¨≤ŗ£©£¨«ů÷§£ļ ![]() «∂®÷Ķ£Ľ
«∂®÷Ķ£Ľ
£®ĘÚ£©…ŤŇ◊őÔŌŖ![]() ‘ŕ
‘ŕ![]() ļÕ
ļÕ![]() Ķ„Ķń«–ŌŖĹĽ”ŕĶ„
Ķ„Ķń«–ŌŖĹĽ”ŕĶ„![]() £¨ ‘ő £ļ
£¨ ‘ő £ļ ![]() ÷Š…Ō «∑Ůīś‘ŕĶ„
÷Š…Ō «∑Ůīś‘ŕĶ„![]() £¨ ĻĶ√
£¨ ĻĶ√![]() ő™Ń‚–ő£Ņ»Űīś‘ŕ£¨«ŽňĶ√ųņŪ”…≤Ę«ůīň Ī÷ĪŌŖ
ő™Ń‚–ő£Ņ»Űīś‘ŕ£¨«ŽňĶ√ųņŪ”…≤Ę«ůīň Ī÷ĪŌŖ![]() Ķń–Ī¬ ļÕĶ„
Ķń–Ī¬ ļÕĶ„![]() Ķń◊ÝĪÍ£ģ
Ķń◊ÝĪÍ£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņľ◊°Ę““ŃĹ»ňÕś◊™ŇŐ”őŌ∑£¨ł√”őŌ∑Ļś‘Ú «’‚—ýĶń£ļ“ĽłŲ÷ Ķōĺý‘»ĶńĪÍ”–12Ķ»∑÷ ż◊÷łŮĶń◊™ŇŐ£®»ÁÕľ£©£¨ľ◊°Ę““ŃĹ»ňłų◊™◊™ŇŐ“Ľīő£¨◊™ŇŐÕ£÷Ļ Ī÷ł’Žňý÷łĶń ż◊÷ő™ł√»ňĶńĶ√∑÷£ģ£®ľŔ…Ť÷ł’Ž≤Ľń‹÷łŌÚ∑÷ĹÁŌŖ£©Ō÷ľ◊Ō»◊™£¨““ļů◊™£¨«ůŌ¬Ń– ¬ľĢ∑Ę…ķĶńłŇ¬ 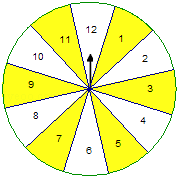
£®1£©ľ◊Ķ√∑÷≥¨Ļż7∑÷ĶńłŇ¬ £ģ
£®2£©ľ◊Ķ√7∑÷£¨«“““Ķ√10∑÷ĶńłŇ¬
£®3£©ľ◊Ķ√5∑÷«“ĽŮ §ĶńłŇ¬ £ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°ŅļĮ żf£®x£©= ![]() +lg£®2x+1£©Ķń∂®“Ś”Úő™£® £©
+lg£®2x+1£©Ķń∂®“Ś”Úő™£® £©
A.£®©Ā5£¨+°ř£©
B.[©Ā5£¨+°ř£©
C.£®©Ā5£¨0£©
D.£®©Ā2£¨0£©
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľňý ĺ£¨‘໿ņ‚◊∂P £≠ABC÷–£¨PA°ÕĶ◊√śABC£¨°ŌBCA![]() 90°„£¨AP
90°„£¨AP![]() AC£¨Ķ„D£¨E∑÷Īū‘ŕņ‚PB£¨PC…Ō£¨«“BC°ő∆Ĺ√śADE.
AC£¨Ķ„D£¨E∑÷Īū‘ŕņ‚PB£¨PC…Ō£¨«“BC°ő∆Ĺ√śADE.

£®ĘŮ£©«ů÷§£ļDE°Õ∆Ĺ√śPAC£Ľ
£®ĘÚ£©»ŰPC°ÕAD£¨«“»żņ‚◊∂P£≠ABCĶńŐŚĽżő™8£¨«ů∂ŗ√śŐŚABCEDĶńŐŚĽż£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™tan¶Ń£¨ ![]() «Ļō”ŕxĶń∑Ĺ≥Őx2©Ākx+k2©Ā3=0ĶńŃĹ Ķłý£¨«“3¶–£ľ¶Ń£ľ
«Ļō”ŕxĶń∑Ĺ≥Őx2©Ākx+k2©Ā3=0ĶńŃĹ Ķłý£¨«“3¶–£ľ¶Ń£ľ ![]() ¶–£¨«ůcos£®3¶–+¶Ń£©©Āsin£®¶–+¶Ń£©Ķń÷Ķ£ģ
¶–£¨«ůcos£®3¶–+¶Ń£©©Āsin£®¶–+¶Ń£©Ķń÷Ķ£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ļķľ —ß–£”Ň—° - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com