
分析 (Ⅰ)通过讨论x的范围求出各个区间上的不等式的解集,取并集即可;(Ⅱ)根据绝对值的性质,得到关于a的不等式,解出即可.
解答 解:(Ⅰ)不等式f(x)+x>0可化为|x-2|+x>|x+1|,
当x<-1时,-(x-2)+x>-(x+1),解得x>-3,即-3<x<-1;
当-1≤x≤2时,-(x-2)+x>x+1,解得x<1,即-1≤x<1;
当x>2时,x-2+x>x+1,解得:x>3,即x>3,
综上所述,不等式f(x)+x>0的解集为{x|-3<x<1或x>3}.…(5分)
(Ⅱ)由不等式f(x)≤a2-2a,
可得|x-2|-|x+1|≤a2-2a,
∵|x-2|-|x+1|≤|x-2-x-1|=3,
∴a2-2a≥3,即a2-2a-3≥0,解得a≤-1或a≥3,
故实数a的取值范围是a≤-1或a≥3.…(10分)
点评 本题考查了解绝对值不等式问题,考查绝对值的性质,是一道中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
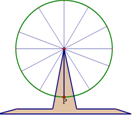 一个均速旋转的摩天轮每12分钟逆时针旋转一周,最低点距地面2米,最高点距地面18米,甲从摩天轮最低点处上摩天轮,3分钟后乙也在其最低点处上摩天轮,从乙上摩天轮开始计时,在摩天轮转动的一圈内,有3分钟,甲、乙距地面的高度之和不小于28米.
一个均速旋转的摩天轮每12分钟逆时针旋转一周,最低点距地面2米,最高点距地面18米,甲从摩天轮最低点处上摩天轮,3分钟后乙也在其最低点处上摩天轮,从乙上摩天轮开始计时,在摩天轮转动的一圈内,有3分钟,甲、乙距地面的高度之和不小于28米.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 “杨辉三角形”是古代重要的数学成就,它比西方的“帕斯卡三角形”早了300多年,如图是三角形数阵,记an为图中第n行各个数之和,则a5+a11的值为( )
“杨辉三角形”是古代重要的数学成就,它比西方的“帕斯卡三角形”早了300多年,如图是三角形数阵,记an为图中第n行各个数之和,则a5+a11的值为( )| A. | 528 | B. | 1020 | C. | 1038 | D. | 1040 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
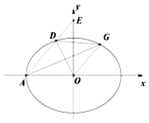 如图,在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点为A(-2,0),离心率为$\frac{\sqrt{2}}{2}$,过A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴为E,过点O作直线l的平行线交椭圆于点G,设△AOD,△AOE,△DOG的面积分别为S1、S2、S3.
如图,在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点为A(-2,0),离心率为$\frac{\sqrt{2}}{2}$,过A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴为E,过点O作直线l的平行线交椭圆于点G,设△AOD,△AOE,△DOG的面积分别为S1、S2、S3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,$\frac{2\sqrt{10+3\sqrt{3}}}{3}$] | B. | [2,$\frac{8}{3}$] | C. | [0,$\frac{2\sqrt{13}}{3}$] | D. | [2,$\frac{2\sqrt{13}}{3}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com