
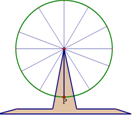
 一个均速旋转的摩天轮每12分钟逆时针旋转一周,最低点距地面2米,最高点距地面18米,甲从摩天轮最低点处上摩天轮,3分钟后乙也在其最低点处上摩天轮,从乙上摩天轮开始计时,在摩天轮转动的一圈内,有3分钟,甲、乙距地面的高度之和不小于28米.
一个均速旋转的摩天轮每12分钟逆时针旋转一周,最低点距地面2米,最高点距地面18米,甲从摩天轮最低点处上摩天轮,3分钟后乙也在其最低点处上摩天轮,从乙上摩天轮开始计时,在摩天轮转动的一圈内,有3分钟,甲、乙距地面的高度之和不小于28米. 分析 由题意,设乙与地面高度与时间t的关系,f(t)=Asin(ωt+φ)+B(A>0,ω>0,φ∈[0,2π)),求出f(t)的解析式,甲,乙时间t的关系是t+3.甲、乙距地面的高度之和不小于28米,建立不等式关系即可求解,时间t范围.可得答案.
解答 解:设乙与地面高度与时间t的关系,f(t)=Asin(ωt+φ)+B(A>0,ω>0,φ∈[0,2π)),
由题意可知:A=8,B=10,T=12,∴ω=$\frac{π}{6}$.
即f(t)=8sin($\frac{π}{6}$t+φ)+10,
又∵f(0)=2,φ∈[0,2π),
故φ=$\frac{3π}{2}$
得 f(t)=8sin($\frac{π}{6}$t$+\frac{3π}{2}$)+10.
当乙在最低点时,距离地面高度2米.此时甲距离地面的高度为:10+8sin($\frac{π}{6}×3$+$\frac{3π}{2}$)=10米.
设t分钟后甲、乙距地面的高度之和不小于28米,
则:8sin($\frac{π}{6}$t$+\frac{3π}{2}$)+10+8sin[$\frac{π}{6}$(t+3)$+\frac{3π}{2}$]+10≥28.(0≤t<12)
化简可得:sin$\frac{π}{6}t$-cos$\frac{π}{6}t$≥1,
即$\sqrt{2}$sin($\frac{π}{6}t-\frac{π}{4}$)≥1,
∴$\frac{π}{4}$$≤\frac{π}{6}t-\frac{π}{4}≤\frac{3π}{4}$,
故得:3≤t≤6.
即从乙上摩天轮开始计时,3分钟后,甲、乙距地面的高度之和不小于28米,6分钟后甲、乙距地面的高度之和小于28米.
在摩天轮转动的一圈内,有3分钟甲、乙距地面的高度之和不小于28米.
故答案为3.
点评 本题考查通过实际问题得到三角函数的性质,由性质求三角函数的解析式;考查y=Asin(ωx+φ)中参数的物理意义,注意三角函数的模型的应用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
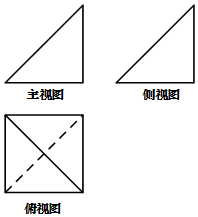 某空间几何体的三视图如图所示,图中主视图和侧视图是两个全等的等腰直角三角形,腰长为4,俯视图中的四边形为正方形,则这个几何体的体积是( )
某空间几何体的三视图如图所示,图中主视图和侧视图是两个全等的等腰直角三角形,腰长为4,俯视图中的四边形为正方形,则这个几何体的体积是( )| A. | $\frac{32}{3}$ | B. | $\frac{64}{3}$ | C. | 16 | D. | 32 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -f(x) | B. | f(x) | C. | g(x) | D. | -g(x) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com