练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．如下等式：

    以此类推，则2018出现在第31个等式中．

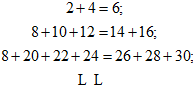
    分析 从已知等式分析，发现规律为：各等式首项分别为2×1，2（1+3），2（1+3+5），…，即可得出结论．

    解答 解：①2+4=6；  
    ②8+10+12=14+16；
    ③18+20+22+24=26+28+30，…
    其规律为：各等式首项分别为2×1，2（1+3），2（1+3+5），…，
    所以第n个等式的首项为2[1+3+…+（2n-1）]=2×$\frac{n（1+2n-1）}{2}$=2n2，
    当n=31时，等式的首项为2×312=1932，
    当n=32时，等式的首项为2×322=2048，
    所以2018在第31个等式中，
    故答案为：31

    点评 本题考查归纳推理，难点是根据能够找出数之间的内在规律，考查观察、分析、归纳的能力，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    14．若圆（x-3）2+（y+5）2=r2上恰有3个点到直线4x-3y=2的距离等于1，则半径r的值为6．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．执行如图所示的程序框图，输出的S值为（　　）
    A．$-\frac{{\sqrt{3}}}{2}$B．0C．$\sqrt{3}$D．$\frac{{\sqrt{3}}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．一个均速旋转的摩天轮每12分钟逆时针旋转一周，最低点距地面2米，最高点距地面18米，甲从摩天轮最低点处上摩天轮，3分钟后乙也在其最低点处上摩天轮，从乙上摩天轮开始计时，在摩天轮转动的一圈内，有3分钟，甲、乙距地面的高度之和不小于28米．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

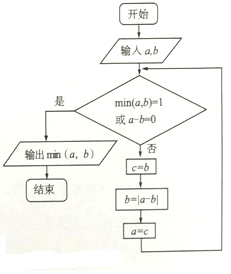    19．min（a，b）表示a，b中的最小值，执行如图所示的程序框图，若输入的a，b值分别为4，10，则输出的min（a，b）值是（　　）
    A．0B．1C．2D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．甲、乙两人进行射击比赛，各射击4局，每局射击10次，射击命中目标得1分，未命中目标得0分．两人4局的得分情况如下：
     甲 6 6 9 9
     乙 7 9 x y
    （1）已知在乙的4局比赛中随机选取1局时，此局得分小于6分的概率不为零，且在4局比赛中，乙的平均得分高于甲的平均得分，求x+y的值；
    （2）如果x=6，y=10，从甲、乙两人的4局比赛中随机各选取1局，并将其得分分别记为a，b，求a＞b的概率；
    （3）在4局比赛中，若甲、乙两人的平均得分相同，且乙的发挥更稳定，写出x的所有可能取值．（结论不要求证明）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．设等比数列{an}中，前n项和为Sn，已知S3=8，S6=4，则S12=5．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知函数f（x）=$\frac{1}{2}$x2，g（x）=elnx
    （1）设函数F（x）=f（x）-g（x），求F（x）的单调区间并求最小值；
    （2）若存在常数k，m，使得f（x）≥kx+m对x∈R恒成立，且g（x）≤kx+m对x∈（0，+∞）恒成立，则称直线y=kx+m为函数f（x）与g（x）的“分界线”，试问：f（x）与g（x）是否存在“分界线”？若存在，求出“分界线”的方程，若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知${（{\frac{3}{{\sqrt{a}}}-\root{3}{a}}）^n}$的展开式的各项系数之和等于${（{4\root{3}{b}-\frac{1}{{\sqrt{5b}}}}）^5}$展开式中的常数项，求${（{\frac{3}{{\sqrt{a}}}-\root{3}{a}}）^n}$展开式中含$\frac{1}{a}$的项的二项式系数．

    查看答案和解析>>

    同步练习册答案