
| �� | 6 | 6 | 9 | 9 |
| �� | 7 | 9 | x | y |
���� ��1�����ҵ�ƽ���÷ָ��ڼ�ƽ���÷֣����x+y��14���Ƶ���x��y������һ��С��6���ɴ������x+y��
��2���衰�Ӽס��ҵ�4�ֱ����������ѡȡ1�֣��ҵ÷�����a��b��Ϊ�¼�M���Ǽ�4�ֱ���ΪA1��A2��A3��A4�����ֵĵ÷ֱַ���6��6��9��9���ҵ�4�ֱ���ΪB1��B2��B3��B4�����ֵĵ÷ֱַ���7��9��6��10����Ӽס��ҵ�4�ֱ����������ѡȡ1�֣������оٷ������a��b�ĸ��ʣ�
��3���ɼס������˵�ƽ���÷���ͬ�����ҵķ��Ӹ��ȶ�����д��x�����п��ܣ�
��� �⣺��1���������$\frac{7+9+x+y}{4}��\frac{6+6+9+9}{4}$����x+y��14��
�����ҵ�4�ֱ��������ѡȡ1��ʱ���˾ֵ÷�С�ڣ�6�֣��ĸ��ʲ�Ϊ�㣬
��x��y������һ��С��6���֡�x��10��y��10����x��y��N��
��x+y��15����x+y=15��
��2���衰�Ӽס��ҵ�4�ֱ����������ѡȡ1�֣��ҵ÷�����a��b��Ϊ�¼�M��
�Ǽ�4�ֱ���ΪA1��A2��A3��A4�����ֵĵ÷ֱַ���6��6��9��9��
�ҵ�4�ֱ���ΪB1��B2��B3��B4�����ֵĵ÷ֱַ���7��9��6��10��
��Ӽס��ҵ�4�ֱ����������ѡȡ1�֣����п��ܵĽ����16�֣������ǣ�
��A1��B1������A1��B2������A1��B3������A1��B4������A2��B1������A2��B2����
��A2��B3������A2��B4������A3��B1������A3��B2������A3��B3������A3��B4����
��A4��B1������A4��B2������A4��B3������A4��B4����
���¼�M�Ľ����4�֣������ǣ�
��A3��B1������A3��B3������A4��B1������A4��B3����
���¼�M�ĸ���P��M��=$\frac{4}{16}=\frac{1}{4}$��
��3��x�����п���ȡֵΪ6��7��8��
���� ���⿼��Ƶ�ʷֲ�ֱ��ͼ��Ӧ�ã�������ʵ����漰��Ƶ�ʷֲ�ֱ��ͼ�Ȼ���֪ʶ������������֤����������������������黯����ת��˼�롢���ν��˼�룬�ǻ����⣮


 ̽���빮�̺��Ͽ�ѧ����������ϵ�д�
̽���빮�̺��Ͽ�ѧ����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4+$\sqrt{2}$+$\sqrt{6}$ | B�� | 3+$\sqrt{2}$+$\sqrt{3}$ | C�� | 2+$\sqrt{2}$ | D�� | 3+$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
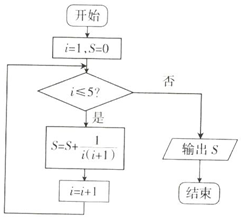
| A�� | $\frac{5}{6}$ | B�� | $\frac{4}{5}$ | C�� | $\frac{6}{7}$ | D�� | $\frac{7}{8}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{2}$ | B�� | $\sqrt{3}$ | C�� | 3 | D�� | $2\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
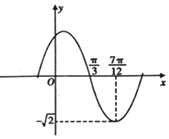 ����f��x��=Asin����x+�գ�����A���أ����dz�����A��0���أ�0��|��|��$\frac{��}{2}$���IJ���ͼ����ͼ��ʾ����y=f��x����x��[-$\frac{��}{4}$��$\frac{��}{2}$]�ϵ�ȡֵ��Χ�ǣ�������
����f��x��=Asin����x+�գ�����A���أ����dz�����A��0���أ�0��|��|��$\frac{��}{2}$���IJ���ͼ����ͼ��ʾ����y=f��x����x��[-$\frac{��}{4}$��$\frac{��}{2}$]�ϵ�ȡֵ��Χ�ǣ�������| A�� | [-$\frac{\sqrt{2}}{2}$��$\sqrt{2}$] | B�� | [$\frac{\sqrt{2}}{2}$��$\sqrt{2}$] | C�� | [-$\frac{\sqrt{6}}{2}$��$\sqrt{2}$] | D�� | [$\frac{\sqrt{6}}{2}$��$\sqrt{2}$] |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com