
分析 设双曲线的一条渐近线方程为y=$\frac{b}{a}$x,P在x轴上方,Q在x轴的下方,H为PQ的中点,运用圆的垂径定理和点到直线的距离公式可得FH=b,再由向量数量积的定义可得∠PFQ=120°,进而判断PF⊥OF,求得c=2a,PQ=6a,OP=4a,OQ=2a,进而得到λ,由P在x轴下方,Q在x轴的上方,可得λ的另一个值.
解答 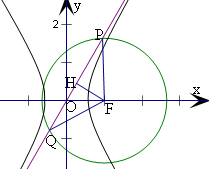 解:设双曲线的一条渐近线方程为y=$\frac{b}{a}$x,
解:设双曲线的一条渐近线方程为y=$\frac{b}{a}$x,
P在x轴上方,Q在x轴的下方,
H为PQ的中点,可得FH⊥PQ,
由F(c,0)到渐近线的距离为d=$\frac{bc}{\sqrt{{a}^{2}+{b}^{2}}}$=b,
由$\overrightarrow{FP}$•$\overrightarrow{FQ}$=-6a2,可得2$\sqrt{3}$a•2$\sqrt{3}$a•cos∠PFQ=-6a2,
解得∠PFQ=120°,
FH=b=2$\sqrt{3}$a•cos60°=$\sqrt{3}$a,
则渐近线的斜率为$\sqrt{3}$,∠POF=60°,
由∠OPF=30°,可得PF⊥OF,
则c=2$\sqrt{3}$a•$\frac{\sqrt{3}}{3}$=2a,
OP=2c=4a,OQ=PQ-OP=2PH-4a=2•2$\sqrt{3}$a•$\frac{\sqrt{3}}{2}$-4a=2a,
由$\overrightarrow{OP}=λ\overrightarrow{OQ}$,可得λ<0,
且λ=-2;
当P在x轴下方,Q在x轴的上方,
可得λ=-$\frac{1}{2}$.
即有λ=-2或-$\frac{1}{2}$.
故答案为:-2或-$\frac{1}{2}$.
点评 本题考查双曲线的方程和性质,主要是渐近线方程的运用,考查直线和圆的位置关系,以及平面几何中圆的性质,考查点到直线的距离公式和向量的数量积的定义和向量共线的性质,属于中档题.


科目:高中数学 来源: 题型:选择题
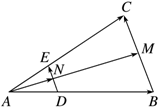 如图,在△ABC中,$\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AB}$,DE∥BC交AC于E,BC边上的中线AM交DE于N,设$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AC}$=$\overrightarrow{b}$,用$\overrightarrow a$,$\overrightarrow{b}$表示向量$\overrightarrow{AN}$.则$\overrightarrow{AN}$等于( )
如图,在△ABC中,$\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AB}$,DE∥BC交AC于E,BC边上的中线AM交DE于N,设$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AC}$=$\overrightarrow{b}$,用$\overrightarrow a$,$\overrightarrow{b}$表示向量$\overrightarrow{AN}$.则$\overrightarrow{AN}$等于( )| A. | $\frac{1}{2}$($\overrightarrow a$+$\overrightarrow{b}$) | B. | $\frac{1}{3}$( $\overrightarrow a$+$\overrightarrow{b}$) | C. | $\frac{1}{6}$( $\overrightarrow a$+$\overrightarrow{b}$) | D. | $\frac{1}{8}$( $\overrightarrow a$+$\overrightarrow{b}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 把正整数按一定的规律排成如图所示的三角形数阵.设aij(i,j∈N*)是位于数阵中从上向下数第i行,从左向右数第j列的数,例如:a43=10,若aij=173,则i+j=11.
把正整数按一定的规律排成如图所示的三角形数阵.设aij(i,j∈N*)是位于数阵中从上向下数第i行,从左向右数第j列的数,例如:a43=10,若aij=173,则i+j=11.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
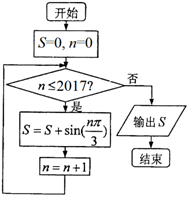
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | 0 | C. | $\sqrt{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
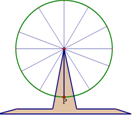 一个均速旋转的摩天轮每12分钟逆时针旋转一周,最低点距地面2米,最高点距地面18米,甲从摩天轮最低点处上摩天轮,3分钟后乙也在其最低点处上摩天轮,从乙上摩天轮开始计时,在摩天轮转动的一圈内,有3分钟,甲、乙距地面的高度之和不小于28米.
一个均速旋转的摩天轮每12分钟逆时针旋转一周,最低点距地面2米,最高点距地面18米,甲从摩天轮最低点处上摩天轮,3分钟后乙也在其最低点处上摩天轮,从乙上摩天轮开始计时,在摩天轮转动的一圈内,有3分钟,甲、乙距地面的高度之和不小于28米.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 甲 | 6 | 6 | 9 | 9 |
| 乙 | 7 | 9 | x | y |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 “杨辉三角形”是古代重要的数学成就,它比西方的“帕斯卡三角形”早了300多年,如图是三角形数阵,记an为图中第n行各个数之和,则a5+a11的值为( )
“杨辉三角形”是古代重要的数学成就,它比西方的“帕斯卡三角形”早了300多年,如图是三角形数阵,记an为图中第n行各个数之和,则a5+a11的值为( )| A. | 528 | B. | 1020 | C. | 1038 | D. | 1040 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com