
分析 (1)根据椭圆的性质,及椭圆的通径,即可求得a和b的值;
(2)分别求得直线A1M,A2M的方程,代入椭圆方程,即可求得P,Q坐标,根据直线的斜率公式,即可求得直线PQ是否恒过定点.
解答 解:(1)由题意的焦点在x轴上,设椭圆方程:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),
由e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{\sqrt{3}}{2}$,则a2=4b2,由题意的通径$\frac{2{b}^{2}}{a}$=1,
解得:a=2,b=1,
∴椭圆的标准方程:$\frac{{x}^{2}}{4}+{y}^{2}=1$;
(2)由(1)知椭圆C的标准方程为$\frac{{x}^{2}}{4}+{y}^{2}=1$,则A1(-2,0),A2(2,0),
M(-4,m)(m∈R,且m≠0)P(x1,y1).Q(x2,y2)
${k}_{{A}_{1}M}$=$\frac{m-0}{-4+2}$=-$\frac{m}{2}$,${k}_{{A}_{2}M}$=$\frac{m-0}{-4-2}$=-$\frac{m}{6}$,
∴A1M:y=-$\frac{m}{2}$(x+2),A2M:y=-$\frac{m}{6}$(x-2),
$\left\{\begin{array}{l}{y=-\frac{m}{2}(x+2)}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,整理得:(m2+1)x2+4m2x+4m2-4=0,
-2x1=$\frac{4{m}^{2}-4}{{m}^{2}+1}$,x1=-$\frac{2{m}^{2}-2}{{m}^{2}+1}$,y1=-$\frac{m}{2}$(x1+2)=-$\frac{2m}{{m}^{2}+1}$,
P(-$\frac{2{m}^{2}-2}{{m}^{2}+1}$,-$\frac{2m}{{m}^{2}+1}$),
由$\left\{\begin{array}{l}{y=-\frac{m}{6}(x-2)}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,消去y得:(m2+9)x2-4m2x+4m2-36=0,
∴2x2=$\frac{4{m}^{2}-36}{{m}^{2}+9}$,∴x2=$\frac{2{m}^{2}-18}{{m}^{2}+9}$,y2=-$\frac{m}{6}$(x2-2)=$\frac{6m}{{m}^{2}+9}$,
Q($\frac{2{m}^{2}-18}{{m}^{2}+9}$,$\frac{6m}{{m}^{2}+9}$).
则kPQ=kPQ=$\frac{2m}{3-{m}^{2}}$(m≠±$\sqrt{3}$),y+$\frac{2m}{{m}^{2}+1}$=$\frac{2m}{3-{m}^{2}}$(x+$\frac{2{m}^{2}-2}{{m}^{2}+1}$),
y=$\frac{2m}{3-{m}^{2}}$x-$\frac{2m}{{m}^{2}+1}$=$\frac{2m}{3-{m}^{2}}$(x+1),
∴直线PQ恒过定点(-1,0),
当m=$\sqrt{3}$时,P(-1,-$\frac{\sqrt{3}}{2}$),Q(-1,$\frac{\sqrt{3}}{2}$),当m=-$\sqrt{3}$时,P(-1,$\frac{\sqrt{3}}{2}$),Q(-1,-$\frac{\sqrt{3}}{2}$),
直线PQ恒过定点(-1,0),
∴综上可知:直线PQ恒过定点(-1,0),
点评 通过直线与圆锥曲线的位置关系处理,考查学生的运算能力.通过方程与几何问题的综合,考查学生分析转化问题的能力,探究研究问题的能力,并体现了合理消元,设而不解的代数变形的思想,属于中档题.


科目:高中数学 来源: 题型:选择题
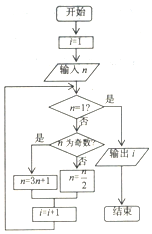 20世纪70年代,流行一种游戏---角谷猜想,规则如下:任意写出一个自然数n,按照以下的规律进行变换:如果n是个奇数,则下一步变成3n+1;如果n是个偶数,则下一步变成$\frac{n}{2}$,这种游戏的魅力在于无论你写出一个多么庞大的数字,最后必然会落在谷底,更准确的说是落入底部的4-2-1循环,而永远也跳不出这个圈子,下列程序框图就是根据这个游戏而设计的,如果输出的i值为6,则输入的n值为( )
20世纪70年代,流行一种游戏---角谷猜想,规则如下:任意写出一个自然数n,按照以下的规律进行变换:如果n是个奇数,则下一步变成3n+1;如果n是个偶数,则下一步变成$\frac{n}{2}$,这种游戏的魅力在于无论你写出一个多么庞大的数字,最后必然会落在谷底,更准确的说是落入底部的4-2-1循环,而永远也跳不出这个圈子,下列程序框图就是根据这个游戏而设计的,如果输出的i值为6,则输入的n值为( )| A. | 5 | B. | 16 | C. | 5或32 | D. | 4或5或32 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
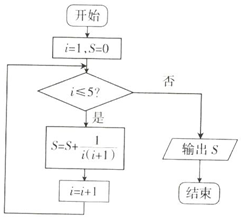
| A. | $\frac{5}{6}$ | B. | $\frac{4}{5}$ | C. | $\frac{6}{7}$ | D. | $\frac{7}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
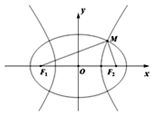 已知椭圆C1:$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{{p}^{2}}$=1(m>p>0)与双曲线C2:$\frac{{x}^{2}}{{n}^{2}}$-$\frac{{y}^{2}}{{p}^{2}}$=1(n>0)有公共的焦点F1,F2,设M为C1与C2在第一象限内的交点,|F1F2|=2c.则( )
已知椭圆C1:$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{{p}^{2}}$=1(m>p>0)与双曲线C2:$\frac{{x}^{2}}{{n}^{2}}$-$\frac{{y}^{2}}{{p}^{2}}$=1(n>0)有公共的焦点F1,F2,设M为C1与C2在第一象限内的交点,|F1F2|=2c.则( )| A. | m2+n2=2c2,且∠F1MF2>$\frac{π}{2}$ | B. | m2+n2=2c2,且∠F1MF2=$\frac{π}{2}$ | ||
| C. | m2+n2=4c2,且∠F1MF2>$\frac{π}{2}$ | D. | m2+n2=4c2,且∠F1MF2=$\frac{π}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com