
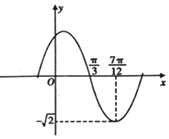
 函数f(x)=Asin(ωx+φ),(A,ω,φ是常数,A>0,ω>0,|φ|≤$\frac{π}{2}$)的部分图象如图所示,则y=f(x)在x∈[-$\frac{π}{4}$,$\frac{π}{2}$]上的取值范围是( )
函数f(x)=Asin(ωx+φ),(A,ω,φ是常数,A>0,ω>0,|φ|≤$\frac{π}{2}$)的部分图象如图所示,则y=f(x)在x∈[-$\frac{π}{4}$,$\frac{π}{2}$]上的取值范围是( )| A. | [-$\frac{\sqrt{2}}{2}$,$\sqrt{2}$] | B. | [$\frac{\sqrt{2}}{2}$,$\sqrt{2}$] | C. | [-$\frac{\sqrt{6}}{2}$,$\sqrt{2}$] | D. | [$\frac{\sqrt{6}}{2}$,$\sqrt{2}$] |
分析 由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式;再利用正弦函数的定义域和值域,求得f(x)的范围.
解答 解:根据函数f(x)=Asin(ωx+φ),(A,ω,φ是常数,A>0,ω>0,|φ|≤$\frac{π}{2}$)的部分图象,
可得A=$\sqrt{2}$,$\frac{T}{4}$=$\frac{7π}{12}$-$\frac{π}{3}$=$\frac{1}{4}•\frac{2π}{ω}$,∴ω=2,再根据五点法作图可得2•$\frac{π}{3}$+φ=π,
∴φ=$\frac{π}{3}$,函数f(x)=$\sqrt{2}$sin(2x+$\frac{π}{3}$).
∵x∈[-$\frac{π}{4}$,$\frac{π}{2}$],∴2x+$\frac{π}{3}$∈[-$\frac{π}{6}$,$\frac{4π}{3}$],
∴sin(2x+$\frac{π}{3}$)∈[-$\frac{\sqrt{3}}{2}$,1],∴f(x)∈[-$\frac{\sqrt{6}}{2}$,$\sqrt{2}$],
故选:C.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,正弦函数的定义域和值域,属于基础题.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:高中数学 来源: 题型:解答题
| 甲 | 6 | 6 | 9 | 9 |
| 乙 | 7 | 9 | x | y |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 “杨辉三角形”是古代重要的数学成就,它比西方的“帕斯卡三角形”早了300多年,如图是三角形数阵,记an为图中第n行各个数之和,则a5+a11的值为( )
“杨辉三角形”是古代重要的数学成就,它比西方的“帕斯卡三角形”早了300多年,如图是三角形数阵,记an为图中第n行各个数之和,则a5+a11的值为( )| A. | 528 | B. | 1020 | C. | 1038 | D. | 1040 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({0,\frac{3}{4}})$ | B. | $({0,\frac{1}{4}}]$ | C. | $[{\frac{1}{4},\frac{3}{4}}]$ | D. | $[{\frac{3}{4},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | 1 | C. | 2 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com