
分析 (1)由椭圆的离心率公式,求得a=2c,b2=a2-c2=2c2,由函数的对称性可知:ME的直线方程为y=x+1,代入椭圆方程,由△=0,即可求得c值,即可求得a和b,求得椭圆方程;
(2)设l的方程,代入椭圆方程,利用韦达定理及向量数量积的坐标运算,即可求得t的范围.
解答 解:(1)由题意的椭圆的离心率e=$\frac{c}{a}$=$\frac{1}{2}$,则a=2c,b2=a2-c2=2c2,
由椭圆的对称性,不妨设在x轴上方的切点为M,x轴下方的切点为N,则kME=1,ME的直线方程为y=x+1,
所以$\left\{{\begin{array}{l}{y=x+\sqrt{7}}\\{\frac{x^2}{{4{c^2}}}+\frac{y^2}{{3{c^2}}}=1}\end{array}}\right.$,整理得:7x2+8$\sqrt{7}$x+28-12c2=0
△=(8$\sqrt{7}$)2-4×7×(28-12c2)=0,解得:c=1,
∴∴椭圆方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$.
(2)设l的方程为x=my+t,A(x1,y1),B(x2,y2),
则$\left\{{\begin{array}{l}{my+t=x}\\{\frac{x^2}{4}+\frac{y^2}{3}=1}\end{array}}\right.$,(3m2+4)y2+6mty+3t2-12=0,
${y_1}+{y_2}=\frac{-6mt}{{3{m^2}+4}},{y_1}{y_2}=\frac{{3{t^2}-12}}{{3{m^2}+4}}$$\overrightarrow{FA}=({x_1}-1,{y_1})$,
$\overrightarrow{FB}=({x_2}-1,{y_2})$,$\overrightarrow{FA}$•$\overrightarrow{FB}$=(x2-1)(x1-1)+y1y2=x1x2-(x1+x2)+1+y1y2
=$({m^2}+1){y_1}{y_2}+(mt-m)({y_1}+{y_2})+{t^2}-2t+1=0$,
∴7t2-8t-8=9m2有解,
∴7t2-8t-8≥0,则$t≥\frac{{4+6\sqrt{2}}}{7}$或$t≤\frac{{4-6\sqrt{2}}}{7}$.
∴t的范围(-∞,$\frac{4-6\sqrt{2}}{7}$]∪[$\frac{4+6\sqrt{2}}{7}$,+∞).
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,考查韦达定理,向量数量积的坐标运算,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 3 | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
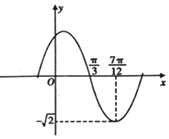 函数f(x)=Asin(ωx+φ),(A,ω,φ是常数,A>0,ω>0,|φ|≤$\frac{π}{2}$)的部分图象如图所示,则y=f(x)在x∈[-$\frac{π}{4}$,$\frac{π}{2}$]上的取值范围是( )
函数f(x)=Asin(ωx+φ),(A,ω,φ是常数,A>0,ω>0,|φ|≤$\frac{π}{2}$)的部分图象如图所示,则y=f(x)在x∈[-$\frac{π}{4}$,$\frac{π}{2}$]上的取值范围是( )| A. | [-$\frac{\sqrt{2}}{2}$,$\sqrt{2}$] | B. | [$\frac{\sqrt{2}}{2}$,$\sqrt{2}$] | C. | [-$\frac{\sqrt{6}}{2}$,$\sqrt{2}$] | D. | [$\frac{\sqrt{6}}{2}$,$\sqrt{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 上春晚次数x(单位:次) | 2 | 4 | 6 | 8 | 10 |
| 粉丝数量y(单位:万人) | 10 | 20 | 40 | 80 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{2}$ | C. | $-\sqrt{2}$ | D. | -2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com