练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．已知Z是复数，|Z-2+i|=$\sqrt{3}$，则|z|的取值范围[$\sqrt{5}-\sqrt{3}$，$\sqrt{5}+\sqrt{3}$]．

    分析 由题意画出图形，求出圆心到原点的距离，数形结合得答案．

    解答 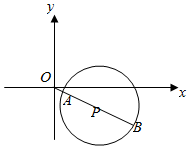解：|Z-2+i|=$\sqrt{3}$的几何意义为复平面内动点Z到定点P（2，-1）的距离为$\sqrt{3}$的轨迹，
    如图：

    ∵|OP|=$\sqrt{5}$，
    ∴|z|的最小值为$\sqrt{5}-\sqrt{3}$，最大值为$\sqrt{5}+\sqrt{3}$．
    取值范围为[$\sqrt{5}-\sqrt{3}$，$\sqrt{5}+\sqrt{3}$]．
    故答案为：[$\sqrt{5}-\sqrt{3}$，$\sqrt{5}+\sqrt{3}$]．

    点评 题考查复数模的求法，考查数形结合的解题思想方法，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    3．若命题p的逆命题是q，否命题是r，则命题q是命题r的（　　）
    A．逆命题B．否命题C．逆否命题D．不等价命题

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知数列{an}前n项和为Sn，等差数列{bn}的前n项和为Tn，且1+3Sn=an+1，a5=256，bn+bn+1=${log}_{\sqrt{2}}$an．
    （1）求数列{an}的通项公式；
    （2）求证：bnbn+1≥Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．a＞0，b＞0且$\frac{1}{a}+\frac{1}{b}=\sqrt{ab}$
    （1）求证a4+b4≥8．
    （2）是否存在a，b使得2a+b=4？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．某班有学生55人，现将所有学生按1，2，3，…，55，随机编号，若采用系统抽样的方法抽取一个容量为5的样本，已知编号为6，a，28，b，50的学生在样本中，则a+b=（　　）
    A．52B．54C．55D．56

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．从双曲线C：b2x2-a2y2=a2b2（a＞0，b＞0）的左焦点F1引圆x2+y2=a2的切线为T，且l交双曲线的右支于点P，若点T是线段F1P的中点，则双曲线C的渐近线方程为2x±y=0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．已知函数f（x）=$\left\{\begin{array}{l}\frac{2}{x}，x＞1\\ 9x{（1-x）^2}，x≤1\end{array}$，若函数g（x）=f（x）-k仅有一个零点，则k的取值范围是（-∞，0）∪（$\frac{4}{3}$，2）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．等差数列{an}的前n项和为Sn，且S2=4，S4=16，数列{bn}满足bn=an+an+1，则数列{bn}的前9和T9=180．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．（1-x-5y）5的展开式中不含x的项的系数和为（　　）（结果化成最简形式）．
    A．1024B．-1024C．1025D．-1028

    查看答案和解析>>

    同步练习册答案