
分析 (1)通过设等差数列{an}的公差为d、等比数列{bn}的公比为q(q>0),利用b2+S3=21、b3=S2联立方程组计算可知q=d=3,进而计算可得结论;
(2)通过(1)及等比、等差数列的求和公式计算可知Tn=$\frac{{3}^{n}-1}{2}$、S15=360,代入化简即得结论.
解答 解:(1)设等差数列{an}的公差为d,等比数列{bn}的公比为q(q>0),
则:b2+S3=b2+3a2=q+3(3+d)=21,q2=3+(3+d),
整理得:$\left\{\begin{array}{l}{q+3d=12}\\{{q}^{2}-d=6}\end{array}\right.$,解得:$\left\{\begin{array}{l}{q=3}\\{d=3}\end{array}\right.$或$\left\{\begin{array}{l}{q=-\frac{10}{3}}\\{d=\frac{46}{9}}\end{array}\right.$(舍),
∴数列{an}是首项、公差均为3的等差数列,数列{bn}是首项为1、公比为3的等比数列,
∴an=3n,bn=3n-1;
(2)由(1)可知Tn=$\frac{1-{3}^{n}}{1-3}$=$\frac{{3}^{n}-1}{2}$,S15=$\frac{15({a}_{1}+{a}_{15})}{2}$=360,
∴不等式4Tn>S15成立等价于4×$\frac{{3}^{n}-1}{2}$>360,即3n>181,
∵34=81<181<35=243,
∴满足条件的最小正整数n=5.
点评 本题考查数列的通项及前n项和,考查运算求解能力,注意解题方法的积累,属于中档题.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 1 | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>0} | B. | {x|0<x<5} | C. | {x|x≥1} | D. | {x|1≤x<5} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1] | B. | [1,+∞) | C. | (-∞,-2] | D. | [-2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
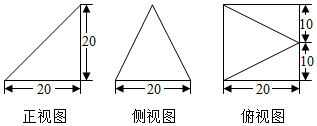
| A. | $\frac{15}{2}$cm | B. | $\frac{15}{4}$cm | C. | $\frac{5\sqrt{41}}{2}$cm | D. | $\frac{5\sqrt{41}}{4}$cm |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com