练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．已知抛物线C：y2=2px（p＞0）与直线l：x=4交于A，B两点，若△OAB的面积为32，则抛物线C的准线方程为（　　）
    A．x=-$\sqrt{2}$B．x=-4C．x=-1D．x=-8

    分析 利用△OAB的面积为32，建立方程，即可求出抛物线C的准线方程．

    解答 解：由题意，x=4，y=±$\sqrt{8p}$，
    ∵△OAB的面积为32，
    ∴$\frac{1}{2}×4×2\sqrt{8p}$=32，
    ∴p=8，
    ∴抛物线C的准线方程为x=-4，
    故选B．

    点评 本题考查抛物线C的准线方程，考查学生的计算能力，比较基础．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    3．某企业生产的某种产品被检测出其中一项质量指标存在问题．该企业为了检查生产该产品的甲，乙两条流水线的生产情况，随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本，测出它们的这一项质量指标值．若该项质量指标值落在（195，210]内，则为合格品，否则为不合格品．表1是甲流水线样本的频数分布表，如图是乙流水线样本的频率分布直方图．
    甲流水线样本的频数分布表
    质量指标值频数
    （190，195]9
    （195，200]10
    （200，205]17
    （205，210]8
    （210，215]6
    （Ⅰ）根据图1，估计乙流水线生产产品该质量指标值的中位数；
    （Ⅱ）若将频率视为概率，某个月内甲，乙两条流水线均生产了5000件产品，则甲，乙两
    条流水线分别生产出不合格品约多少件？
    （Ⅲ）根据已知条件完成下面2×2列联表，并回答是否有85%的把握认为“该企业生产的这
    种产品的质量指标值与甲，乙两条流水线的选择有关”？
    甲生产线乙生产线合计
    合格品
    不合格品
    合计
    附：${K^2}=\frac{{n{{（{ad-bc}）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}$（其中n=a+b+c+d为样本容量）
    P（K2≥k）0.150.100.050.0250.0100.0050.001
    k2.0722.7063.8415.0246.6357.87910.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．若数据x1，x2，…，xn的平均值为$\overline x$，方差为S2，则3x1+5，3x2+5，…，3xn+5的平均值和方差分别为（　　）
    A．$\overline{x}$和S2B．3$\overline{x}$+5和9S2C．3$\overline{x}$+5和S2D．$\overline{x}$和9S2

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．运行如图的程序，输出的结果是-3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．若$\frac{1}{a}＜\frac{1}{b}＜0$，则下列不等式中，正确的不等式有（　　）
    A．a+b＞abB．|a|＞|b|C．a＜bD．$\frac{b}{a}+\frac{a}{b}＞2$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

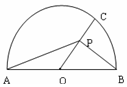    15．如图，半圆的直径AB=4，O为圆心，C为半圆上不同A，B的任意一点，若P为半径OC上的动点，则（$\overrightarrow{PA}+\overline{PB}$）•$\overline{PC}$的最小值等于（　　）
    A．2B．-1C．-2D．0

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．在△ABC中，三边a，b，c与面积S的关系式为S=$\frac{{\sqrt{3}}}{12}（{b^2}+{c^2}-{a^2}）$，则角A等于（　　）
    A．$\frac{π}{2}$B．$\frac{π}{3}$C．$\frac{π}{4}$D．$\frac{π}{6}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知m＞0，p：（x+2）（x-6）≤0，q：2-m≤x≤2+m．
    （1）若p是q的必要条件，求实数m的取值范围
    （2）若m=2，￢p∨￢q为假，求实数x的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．已知函数f（x）=4tanxsin（$\frac{π}{2}$-x）cos（x-$\frac{π}{3}$）-$\sqrt{3}$．
    （Ⅰ）求f（x）的最小正周期；
    （Ⅱ）求f（x）在[-$\frac{π}{4}$，$\frac{π}{4}$]上的单调递增区间．

    查看答案和解析>>

    同步练习册答案