
如图,从A1(1,0,0)、A2(2,0,0)、B1(0,1,0)、B2(0,2,0)、C1(0,0,1)、C2(0,0,2)这6个点中随机选取3个点,将这3个点及原点O两两相连构成一个“立体”,记该“立体”的体积为随机变量V(如果选取的3个点与原点在同一个平面内,此时“立体”的体积V=0).

(1)求V=0的概率;
(2)求V的分布列及数学期望E(V).
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第十章第2课时练习卷(解析版) 题型:填空题
某单位有职工52人,现将所有职工按1、2、3、…、52随机编号,若采用系统抽样的方法抽取一个容量为4的样本,已知6号、32号、45号职工在样本中,则样本中还有一个职工的编号是________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第十一章第6课时练习卷(解析版) 题型:解答题
已知离散型随机变量ξ1的概率分布为
ξ1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
P |
|
|
|
|
|
|
|
离散型随机变量ξ2的概率分布为
ξ2 | 3.7 | 3.8 | 3.9 | 4 | 4.1 | 4.2 | 4.3 |
P |
|
|
|
|
|
|
|
求这两个随机变量数学期望、方差与标准差.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第十一章第5课时练习卷(解析版) 题型:解答题
设进入某商场的每一位顾客购买甲种商品的概率为0.5,购买乙种商品的概率为0.6,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的.
(1)求进入商场的1位顾客购买甲、乙两种商品中的一种的概率;
(2)求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率;
(3)记ξ表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求ξ的分布列.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第十一章第5课时练习卷(解析版) 题型:填空题
省工商局于2003年3月份,对全省流通领域的饮料进行了质量监督抽查,结果显示,某种刚进入市场的x饮料的合格率为80%,现有甲、乙、丙3人聚会,选用6瓶x饮料,并限定每人喝2瓶.则甲喝2瓶合格的x饮料的概率是________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第十一章第4课时练习卷(解析版) 题型:解答题
已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的2个红球和4个黑球.现从甲、乙两个盒内各任取2个球.
(1)求取出的4个球均为黑球的概率;
(2)求取出的4个球中恰有1个红球的概率;
(3)设ξ为取出的4个球中红球的个数,求ξ的分布列.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第十一章第4课时练习卷(解析版) 题型:填空题
设随机变量X的分布列为P(X=k)=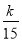 (k=1,2,3,4,5),则P
(k=1,2,3,4,5),则P =________.
=________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第十一章第3课时练习卷(解析版) 题型:解答题
如果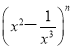 的展开式中,第四项和第七项的二项式系数相等,求:
的展开式中,第四项和第七项的二项式系数相等,求:
(1)展开式的中间项;
(2) 展开式中所有的有理项.
展开式中所有的有理项.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第九章第8课时练习卷(解析版) 题型:解答题
已知双曲线的焦点在x轴上,两个顶点间的距离为2,焦点到渐近线的距离为 .
.
(1)求双曲线的标准方程;
(2)写出双曲线的实轴长、虚轴长、焦点坐标、离心率、渐近线方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com