
【题目】设双曲线与椭圆 ![]() =1有相同的焦点,且与椭圆相交,一个交点A的纵坐标为4,求:
=1有相同的焦点,且与椭圆相交,一个交点A的纵坐标为4,求:
(1)双曲线的标准方程.
(2)若直线L过A(﹣1,2),且与双曲线渐近线y=kx(k>0)垂直,求直线L的方程.
【答案】
(1)解:椭圆 ![]() =1的焦点为(0,3),(0,﹣3),
=1的焦点为(0,3),(0,﹣3),
交点A的纵坐标为4,可得A(± ![]() ,4),
,4),
设双曲线的方程为 ![]() =1(a,b>0),
=1(a,b>0),
由题意可得a2+b2=9, ![]() =1,
=1,
解得a=2,b= ![]() ,
,
则双曲线的方程为 ![]() =1
=1
(2)解:双曲线 ![]() =1的渐近线方程为y=±
=1的渐近线方程为y=± ![]() x,
x,
由题意可得k= ![]() ,
,
则直线l的斜率为﹣ ![]() =﹣
=﹣ ![]() ,
,
即有直线l的方程为y﹣2=﹣ ![]() (x+1),
(x+1),
即为 ![]() x+2y+
x+2y+ ![]() ﹣4=0
﹣4=0
【解析】(1)求得椭圆的焦点,求得A的坐标,设出双曲线的方程,由题意可得a2+b2=9, ![]() =1,解得a,b,即可得到所求方程;(2)求得双曲线的渐近线方程,可得k,由两直线垂直的条件:斜率之积为﹣1,以及点斜式方程即可得到所求方程.
=1,解得a,b,即可得到所求方程;(2)求得双曲线的渐近线方程,可得k,由两直线垂直的条件:斜率之积为﹣1,以及点斜式方程即可得到所求方程.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对的边分别是a,b,c,已知a=2,c= ![]() ,cosA=﹣
,cosA=﹣ ![]() .
.
(1)求sinC和b的值;
(2)求cos(2A+ ![]() )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱柱ABC﹣A1B1C1的侧面AA1C1C为正方形,侧面AA1B1B⊥侧面BB1C1C,且AC=2,AB= ![]() ,∠A1AB=45°,E、F分别为AA1、CC1的中点.
,∠A1AB=45°,E、F分别为AA1、CC1的中点. 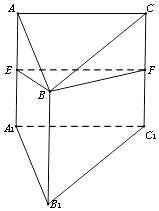
(1)求证:AA1⊥平面BEF;
(2)求二面角B﹣EB1﹣C1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() :
: ![]() (
(![]() )的左右焦点分别为
)的左右焦点分别为![]() ,
, ![]() ,下顶点为
,下顶点为![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.
(Ⅰ)求椭圆![]() 的离心率;
的离心率;
(Ⅱ)设![]() 为椭圆上异于其顶点的一点,
为椭圆上异于其顶点的一点, ![]() 到直线
到直线![]() 的距离为
的距离为![]() ,且三角形
,且三角形![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相切,过焦点
相切,过焦点![]() ,
, ![]() 分别作
分别作![]() ,
, ![]() ,垂足分别为
,垂足分别为![]() ,
, ![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二年级学生会有理科生4名,其中3名男同学;文科生3名,其中有1名男同学.从这7名成员中随机抽4人参加高中示范校验收活动问卷调查.
(Ⅰ)设![]() 为事件“选出的4人中既有文科生又有理科生”,求事件
为事件“选出的4人中既有文科生又有理科生”,求事件![]() 的概率;
的概率;
(Ⅱ)设![]() 为选出的4人中男生人数与女生人数差的绝对值,求随机变量
为选出的4人中男生人数与女生人数差的绝对值,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系 ![]() 中,以原点
中,以原点 ![]() 为极点,以
为极点,以 ![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线 ![]() 的极坐标方程为
的极坐标方程为 ![]() ,曲线
,曲线 ![]() 的参数方程为
的参数方程为 ![]() .
.
(1)求曲线 ![]() 的直角坐标方程与曲线
的直角坐标方程与曲线 ![]() 的普通方程;
的普通方程;
(2)试判断曲线 ![]() 与
与 ![]() 是否存在两个交点?若存在,求出两交点间的距离;若不存在,说明理由.
是否存在两个交点?若存在,求出两交点间的距离;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com