练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
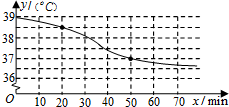
    13．现对复方氨酚烷胺片（中文名：感康）进行深入临床观察，该药物随着进入病人体内的时间与体温的变化情况如图所示，则当时间x从20min到50min时，体温y相对于时间x的平均变化率为（　　）
    A．0.05（℃/min）B．-0.05（℃/min）C．0.025（℃/min）D．-0.025（℃/min）

    分析 利用两个点的坐标，即可求出当时间x从20min到50min时，体温y相对于时间x的平均变化率．

    解答 解：由题意，体温y相对于时间x的平均变化率为$\frac{37-38.5}{50-20}$=-0.05（℃/min）．
    故选：B．

    点评 本题考查平均变化率，考查学生的计算能力，正确运用函数的图象是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    3．全称命题“?a∈Z，a有正因数”的否定是?a∈Z，a没有正因数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．某酒店连续5个月的销售额和利润额资料如下表：
    销售额（x）/万元35679
    利润额（y）/万元23345
    （Ⅰ）画出销售额和利润额的散点图；
    （Ⅱ）如果y对x有线性相关关系，求回归直线方程$\widehat{y}$=bx+a；
    （Ⅲ）如果要求该酒店的利润每月不能少于3.4万元，请你估计一下，这个酒店每月的销售额不得少于多少万元？（参考公式b=$\frac{\sum _{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum _{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，a=$\overline{y}$-b$\overline{x}$）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．已知在平面直角坐标系xOy中圆C的参数方程为$\left\{\begin{array}{l}x=\sqrt{3}+3cosθ\\ y=1+3sinθ.\end{array}$（θ为参数），以原点O为极点，x轴正半轴为极轴建立极坐标系，直线l的极坐标方程为ρcos（θ+$\frac{π}{6}$）=0，则圆C截直线l所得弦长为（　　）
    A．6B．2$\sqrt{2}$C．4$\sqrt{2}$D．$\sqrt{35}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．观察如图算式：
    23=3+5；
    33=7+9+11；
    43=13+15+17+19；
    53=21+23+25+27+29
    …
    203=a1+a2+a3+…，其中a1＜a2＜a3＜…，那么a1=381．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．集合{x∈N|$\frac{3}{3-x}$∈N}的真子集有3个．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．设函数f（x）的导数为f′（x），且f（x）=x2-f′（1）lnx+f′（2），则f′（2）的值是$\frac{7}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．关于等差数列，有下列四个命题：
    （1）若数列中有两项是有理数，则其余各项都是有理数；
    （2）等差数列的通项公式an是关于序号n的一次函数；
    （3）若数列{an}是等差数列，则数列{kan}（k为常数）也是等差数列；
    （4）若数列{an}是等差数列，则数列{an2}也是等差数列．
    其中真命题的个数是（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．已知定义在R上的函数f（x），对任意实数x满足f（x+2）=-f（x-2），且当x∈[0，8）时，f（x）=2x-10，则f（2015）=4．

    查看答案和解析>>

    同步练习册答案