
分析 (1)根据题意可得f(0)=0,由此求得a的值.
(2)利用减函数的定义证明 f(x)是(-3,3)上的减函数.
(3)根据f(k-cosθ)≥f(k2-cos2θ),f(x)是(-3,3)上的减函数,可得 $\left\{\begin{array}{l}{k-cosθ{≤k}^{2}{-cos}^{2}θ}\\{-3<k-cosθ<3}\\{-3{<k}^{2}{-cos}^{2}θ<3}\end{array}\right.$ 对任意的实数θ恒成立,由此分类求得k的范围,综合可得结论.
解答 解:(1)∵函数$f(x)=lg({\frac{a-x}{3+x}})$为奇函数,定义域中包含0,故有f(0)=0,
即lg$\frac{a}{3}$=0,∴a=3.
(2)由(1)可得f(x)=lg$\frac{3-x}{3+x}$,根据$\frac{3-x}{3+x}$>0,求得-3<x<3,故函数的定义域为(-3,3).
(2)任取${x_1},{x_2}∈({-3,3}),且{x_1}<{x_2},f({x_1})-f({x_2})=lg({\frac{{3-{x_1}}}{{3+{x_1}}}})-lg({\frac{{3-{x_2}}}{{3+{x_2}}}})$=$lg\frac{{({3-{x_1}})({3+{x_2}})}}{{({3+{x_1}})({3-{x_2}})}}=lg\frac{{9+3({{x_2}-{x_1}})-{x_1}{x_2}}}{{9+3({{x_1}-{x_2}})-{x_1}{x_2}}}$,
∵9+3(x2-x1)-x1x2>9-x1x2>0,∴$\frac{{9+3({{x_2}-{x_1}})-{x_1}{x_2}}}{{9+3({{x_1}-{x_2}})-{x_1}{x_2}}}>1⇒f({x_1})-f({x_2})>0⇒f({x_1})>f({x_2})$,
∴f(x)是(-3,3)上的减函数.
(3)∵f(k-cosθ)≥-f(cos2θ-k2)=f(k2-cos2θ),f(x)是(-3,3)上的减函数,
∴$\left\{\begin{array}{l}{k-cosθ{≤k}^{2}{-cos}^{2}θ}\\{-3<k-cosθ<3}\\{-3{<k}^{2}{-cos}^{2}θ<3}\end{array}\right.$ 对任意的实数θ恒成立.
由k-cosθ≤cos2θ-k2,可得k-k2≤cosθ-cos2θ对任意的实数θ恒成立.
令y=cosθ-cos2θ=-${(cosθ-\frac{1}{2})}^{2}$+$\frac{1}{4}$,故当cosθ=-1时,y取得最小值为-2,∴k-k2≤-2,
求得k≤-1,或 k≥2 ①.
同理:由-3<k-cosθ<3对θ∈R恒成立得:-2<k<2 ②.
由-3<cos2θ-k2<3对θ∈R恒成立得:$-\sqrt{3}<k<\sqrt{3}$ ③.
综合①②③可得,$-\sqrt{3}<k≤-1$,所以存在这样的k,其范围为$\left\{{k|-\sqrt{3}<k≤-1}\right\}$.
点评 本题主要考查函数的奇偶性、单调性,求函数的最值,函数的恒成立问题,属于中档题.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | b<a<c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
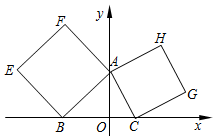 在平面直角坐标系xOy中,已知点A(0,2),B(-2,0),C(1,0),分别以△ABC的边AB、AC向外作正方形ABEF与ACGH,
在平面直角坐标系xOy中,已知点A(0,2),B(-2,0),C(1,0),分别以△ABC的边AB、AC向外作正方形ABEF与ACGH,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | 0 | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{2}$ | C. | $3-\sqrt{3}$ | D. | $3+\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com