
ЁОЬтФПЁПвбжЊЖЏЕу P гыЖЈЕу![]() ЕФОрРыКЭЫќЕНЖЈжБЯп x 4 ЕФОрРыЕФБШЪЧ1: 2 ЃЌМЧЖЏЕу P ЕФЙьМЃЮЊЧњЯп EЃЎ
ЕФОрРыКЭЫќЕНЖЈжБЯп x 4 ЕФОрРыЕФБШЪЧ1: 2 ЃЌМЧЖЏЕу P ЕФЙьМЃЮЊЧњЯп EЃЎ
ЃЈ1ЃЉЧѓЧњЯп E ЕФЗНГЬЃЛ
ЃЈ2ЃЉЩш A ЪЧЧњЯп E ЩЯЕФвЛИіЕуЃЌжБЯп AF НЛЧњЯп E гкСэвЛЕу BЃЌвд AB ЮЊБпзївЛИіЦНааЫФБпаЮЃЌЖЅЕу AЁЂBЁЂCЁЂD ЖМдкЙьМЃ E ЩЯЃЌХаЖЯЦНааЫФБпаЮ ABCD ФмЗёЮЊСтаЮЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЕБЦНааЫФБпаЮ ABCD ЕФУцЛ§ШЁЕНзюДѓжЕЪБЃЌХаЖЯЫќЕФаЮзДЃЌВЂЧѓГіЦфзюДѓжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉВЛФмЪЧСтаЮЃЛЃЈ3ЃЉОиаЮ
ЃЛЃЈ2ЃЉВЛФмЪЧСтаЮЃЛЃЈ3ЃЉОиаЮ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉНЋМИКЮЬѕМўгУзјБъБэЪОГіРДЃЌЛЏМђМДПЩЃЛЃЈ2ЃЉЩшГіжБЯпЗНГЬЃЌСЊСЂЭждВЃЌЕУЕННЛЕузјБъжЎМфЕФЙиЯЕЃЌИљОнСтаЮПЩЕУЖдНЧЯпДЙжБЃЌРћгУЯђСПДІРэЃЛЃЈ3ЃЉаДГіУцЛ§ЃЌРћгУЛЛдЊЗЈЧѓЦфзюДѓжЕЃЌШЗЖЈmЕФжЕЃЌМДПЩХаЖЈЫФБпаЮЕФаЮзДДѓаЁЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЩшЕу![]() ЃЌгЩЬтвтЃК
ЃЌгЩЬтвтЃК ![]() МД
МД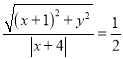 ЃЌЫљвд
ЃЌЫљвд![]() ЛЏМђЕУЃК
ЛЏМђЕУЃК ![]() МДЮЊЧњЯпEЕФЗНГЬ
МДЮЊЧњЯпEЕФЗНГЬ
ЃЈ2ЃЉжБЯпABВЛФмЦНаагкxжсЃЌЙЪЩшжБЯпABЕФЗНГЬЮЊ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]()
гЩ![]() ЕУ
ЕУ![]() ЃЌ Ыљвд
ЃЌ Ыљвд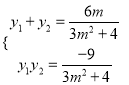 ЂхЂй
ЂхЂй
СЌНсOAЃЌOBЃЌШєABCDЮЊСтаЮЃЌдђ![]() МД
МД![]()
гж![]() ЃЌЫљвдга
ЃЌЫљвдга
![]() ЃЌДњШыЂйЪНЕУ
ЃЌДњШыЂйЪНЕУ![]() ЃЌЮоНтЃЌЙЪABCDВЛФмЪЧСтаЮ.
ЃЌЮоНтЃЌЙЪABCDВЛФмЪЧСтаЮ.
ЃЈ3ЃЉгЩЬтжЊ![]() ЃЌЫљвд
ЃЌЫљвд![]()
Щш![]() ЃЌ
ЃЌ 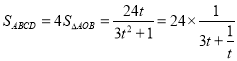
Сю![]() ПЩжЊЕБ
ПЩжЊЕБ![]() ЪБ
ЪБ![]() газюаЁжЕМДУцЛ§газюжЕЃЌДЫЪБ
газюаЁжЕМДУцЛ§газюжЕЃЌДЫЪБ![]() ЃЌМД
ЃЌМД![]() жсЃЌЫљвдABCDЮЊОиаЮ.
жсЃЌЫљвдABCDЮЊОиаЮ.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
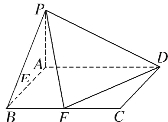
ЁОЬтФПЁПвбжЊдкЫФРтзЖ![]() жаЃЌЕзУц
жаЃЌЕзУц![]() ЪЧОиаЮЃЌЧв
ЪЧОиаЮЃЌЧв![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЦНУц
ЦНУц![]() ЃЌ
ЃЌ![]() ЁЂ
ЁЂ![]() ЗжБ№ЪЧЯпЖЮ
ЗжБ№ЪЧЯпЖЮ![]() ЁЂ
ЁЂ![]() ЕФжаЕуЃЎ
ЕФжаЕуЃЎ
ЃЈ1ЃЉжЄУїЃК![]()
ЃЈ2ЃЉдкЯпЖЮ![]() ЩЯЪЧЗёДцдкЕу
ЩЯЪЧЗёДцдкЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЁЮЦНУц
ЁЮЦНУц![]() ЃЌШєДцдкЃЌШЗЖЈЕу
ЃЌШєДцдкЃЌШЗЖЈЕу![]() ЕФЮЛжУЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЕФЮЛжУЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЃЈ3ЃЉШє![]() гыЦНУц
гыЦНУц![]() ЫљГЩЕФНЧЮЊ
ЫљГЩЕФНЧЮЊ![]() ЃЌЧѓЖўУцНЧ
ЃЌЧѓЖўУцНЧ![]() ЕФгрЯвжЕ
ЕФгрЯвжЕ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВ![]()
![]() ЕФРыаФТЪЮЊ
ЕФРыаФТЪЮЊ![]() ЃЌвддЕуЮЊдВаФЃЌЭждВCЕФЖЬАыжсГЄЮЊАыОЖЕФдВгыжБЯп
ЃЌвддЕуЮЊдВаФЃЌЭждВCЕФЖЬАыжсГЄЮЊАыОЖЕФдВгыжБЯп![]() ЯрЧа.
ЯрЧа.![]() ЁЂ
ЁЂ![]() ЪЧЭждВЕФзѓЁЂгвЖЅЕуЃЌжБЯп
ЪЧЭждВЕФзѓЁЂгвЖЅЕуЃЌжБЯп![]() Й§
Й§![]() ЕуЧвгы
ЕуЧвгы![]() жсДЙжБ.
жсДЙжБ.

ЃЈ1ЃЉЧѓЭждВ![]() ЕФБъзМЗНГЬЃЛ
ЕФБъзМЗНГЬЃЛ
ЃЈ2ЃЉЩш![]() ЪЧЭждВ
ЪЧЭждВ![]() ЩЯвьгк
ЩЯвьгк![]() ЁЂ
ЁЂ![]() ЕФШЮвтвЛЕуЃЌзї
ЕФШЮвтвЛЕуЃЌзї![]() жсгкЕу
жсгкЕу![]() ЃЌбгГЄ
ЃЌбгГЄ![]() ЕНЕу
ЕНЕу![]() ЪЙЕУ
ЪЙЕУ![]() ЃЌСЌНг
ЃЌСЌНг![]() ВЂбгГЄНЛжБЯп
ВЂбгГЄНЛжБЯп![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЕФжаЕуЃЌХаЖЯжБЯп
ЕФжаЕуЃЌХаЖЯжБЯп![]() гывд
гывд![]() ЮЊжБОЖЕФдВ
ЮЊжБОЖЕФдВ![]() ЕФЮЛжУЙиЯЕЃЌВЂжЄУїФуЕФНсТл.
ЕФЮЛжУЙиЯЕЃЌВЂжЄУїФуЕФНсТл.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
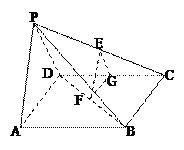
ЁОЬтФПЁПвбжЊжБЯпlгыдВCЃКx2+y2+2xЉ4y+a=0ЯрНЛгкAЃЌBСНЕуЃЌЯвABЕФжаЕуЮЊMЃЈ0ЃЌ1ЃЉЃЎ
ЃЈ1ЃЉШєдВCЕФАыОЖЮЊ![]() ЃЌЧѓЪЕЪ§aЕФжЕЃЛ
ЃЌЧѓЪЕЪ§aЕФжЕЃЛ
ЃЈ2ЃЉШєЯвABЕФГЄЮЊ6ЃЌЧѓЪЕЪ§aЕФжЕЃЛ
ЃЈ3ЃЉЕБa=1ЪБЃЌдВOЃКx2+y2=2гыдВCНЛгкMЃЌNСНЕуЃЌЧѓЯвMNЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫбаОПМвгУНЮГЕдкИпЫйЙЋТЗЩЯЕФГЕЫйЧщПіЃЌНЛЭЈВПУХЖд![]() УћМвгУНЮГЕМнЪЛдБНјааЕїВщЃЌЕУЕНЦфдкИпЫйЙЋТЗЩЯааЪЛЪБЕФЦНОљГЕЫйЧщПіЮЊЃКдк
УћМвгУНЮГЕМнЪЛдБНјааЕїВщЃЌЕУЕНЦфдкИпЫйЙЋТЗЩЯааЪЛЪБЕФЦНОљГЕЫйЧщПіЮЊЃКдк![]() УћФаадМнЪЛдБжаЃЌЦНОљГЕЫйГЌЙ§
УћФаадМнЪЛдБжаЃЌЦНОљГЕЫйГЌЙ§![]()
![]() ЕФга
ЕФга![]() ШЫЃЌВЛГЌЙ§
ШЫЃЌВЛГЌЙ§![]()
![]() ЕФга
ЕФга![]() ШЫЃЛдк
ШЫЃЛдк![]() УћХЎадМнЪЛдБжаЃЌЦНОљГЕЫйГЌЙ§
УћХЎадМнЪЛдБжаЃЌЦНОљГЕЫйГЌЙ§![]()
![]() ЕФга
ЕФга![]() ШЫЃЌВЛГЌЙ§
ШЫЃЌВЛГЌЙ§![]()
![]() ЕФга
ЕФга![]() ШЫ.
ШЫ.
ЃЈЂёЃЉЭъГЩЯТУцЕФСаСЊБэЃЌВЂХаЖЯЪЧЗёга![]() ЕФАбЮеШЯЮЊЦНОљГЕЫйГЌЙ§100
ЕФАбЮеШЯЮЊЦНОљГЕЫйГЌЙ§100![]() гыадБ№гаЙиЃЛ
гыадБ№гаЙиЃЛ
ЦНОљГЕЫйГЌЙ§ | ЦНОљГЕЫйВЛГЌЙ§ | КЯМЦ | |
ФаадМнЪЛШЫЪ§ | |||
ХЎадМнЪЛШЫЪ§ | |||
КЯМЦ |
ЃЈЂђЃЉдкБЛЕїВщЕФМнЪЛдБжаЃЌАДЗжВуГщбљЕФЗНЗЈДгЦНОљГЕЫйВЛГЌЙ§![]()
![]() ЕФШЫжаГщШЁ
ЕФШЫжаГщШЁ![]() ШЫЃЌдйДгет
ШЫЃЌдйДгет![]() ШЫжаВЩгУМђЕЅЫцЛњГщбљЕФЗНЗЈЫцЛњГщШЁ
ШЫжаВЩгУМђЕЅЫцЛњГщбљЕФЗНЗЈЫцЛњГщШЁ![]() ШЫЃЌЧѓет
ШЫЃЌЧѓет![]() ШЫЧЁКУЮЊ
ШЫЧЁКУЮЊ![]() УћФаЩњЁЂ
УћФаЩњЁЂ![]() УћХЎЩњЕФИХТЪ.
УћХЎЩњЕФИХТЪ.
ВЮПМЙЋЪНгыЪ§ОнЃК![]() ЃЌЦфжа
ЃЌЦфжа![]() .
.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙ§ХзЮяЯпy2ЃН2pxЃЈp>0ЃЉЕФНЙЕуЃЌаБТЪЮЊ2![]() ЕФжБЯпНЛХзЮяЯпгкAЃЈx1ЃЌy1ЃЉЃЌBЃЈx2ЃЌy2ЃЉЃЈx1<x2ЃЉСНЕуЃЌЧв|AB|ЃН9ЃЎ
ЕФжБЯпНЛХзЮяЯпгкAЃЈx1ЃЌy1ЃЉЃЌBЃЈx2ЃЌy2ЃЉЃЈx1<x2ЃЉСНЕуЃЌЧв|AB|ЃН9ЃЎ
ЃЈ1ЃЉЧѓИУХзЮяЯпЕФЗНГЬЃЎ
ЃЈ2ЃЉOЮЊзјБъдЕуЃЌCЮЊХзЮяЯпЩЯвЛЕуЃЌШє![]() ЃЌЧѓІЫЕФжЕ
ЃЌЧѓІЫЕФжЕ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈБОаЁЬтТњЗж12ЗжЃЉШчЭМЃЌдкЫФРтзЖ![]() жаЃЌЕзУц
жаЃЌЕзУц![]() ЪЧе§ЗНаЮЃЌВрУц
ЪЧе§ЗНаЮЃЌВрУц![]() ЕзУц
ЕзУц![]() ЃЌЧв
ЃЌЧв![]() ЃЌЩш
ЃЌЩш![]() ЗжБ№ЮЊ
ЗжБ№ЮЊ![]() ЕФжаЕу.
ЕФжаЕу.
ЃЈ1ЃЉЧѓжЄЃКЦНУц![]() ЁЮЦНУц
ЁЮЦНУц![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧѓжЄЃКЦНУц![]() ЦНУц
ЦНУц![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊfЃЈxЃЉЪЧЖЈвхдкЃЈЉЁоЃЌ+ЁоЃЉЩЯЕФХМКЏЪ§ЃЌЧвдкЃЈЉЁоЃЌ0]ЩЯЪЧдіКЏЪ§ЃЌЩшa=fЃЈlog47ЃЉЃЌb=fЃЈlog ![]() 3ЃЉЃЌc=fЃЈ21.6ЃЉЃЌдђaЃЌbЃЌcЕФДѓаЁЙиЯЕЪЧЃЈ ЃЉ
3ЃЉЃЌc=fЃЈ21.6ЃЉЃЌдђaЃЌbЃЌcЕФДѓаЁЙиЯЕЪЧЃЈ ЃЉ
A.cЃМaЃМb
B.cЃМbЃМa
C.bЃМcЃМa
D.aЃМbЃМc
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжааФдкдЕуЃЌНЙЕудкxжсЩЯЕФвЛЭждВгывЛЫЋЧњЯпгаЙВЭЌЕФНЙЕуF1ЃЌF2ЃЌЧв|F1F2|ЃН![]() ЃЌЭждВЕФГЄАыжсгыЫЋЧњЯпЪЕАыжсжЎВюЮЊ4ЃЌРыаФТЪжЎБШЮЊ3ЁУ7.
ЃЌЭждВЕФГЄАыжсгыЫЋЧњЯпЪЕАыжсжЎВюЮЊ4ЃЌРыаФТЪжЎБШЮЊ3ЁУ7.
ЃЈ1ЃЉЧѓетСНЧњЯпЕФЗНГЬЃЛ
ЃЈ2ЃЉШєPЮЊетСНЧњЯпЕФвЛИіНЛЕуЃЌЧѓcosЁЯF1PF2ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com