
分析 根据题意和抛物线以及正三角形的对称性,可推断出两个边的斜率,进而表示出这两条直线,每条直线与抛物线均有两个交点,焦点两侧的两交点连接,分别构成一个等边三角形.进而可知这样的三角形有2个.
解答 解:由y2=2px(P>0)的焦点F($\frac{p}{2}$,0),
等边三角形的一个顶点位于抛物线y2=2px(P>0)的焦点,另外两个顶点在抛物线上,
则等边三角形关于x轴轴对称.
即有两个边的斜率k=±tan30°=±$\frac{\sqrt{3}}{3}$,
其方程为:y=±$\frac{\sqrt{3}}{3}$(x-$\frac{p}{2}$),
每条直线与抛物线均有两个交点,焦点两侧的两交点连接,
分别构成一个等边三角形.
故满足条件的正三角形的个数为2.
故答案为:2.
点评 本题主要考查了抛物线的简单性质,利用抛物线和正三角形的对称性是解题的关键.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{7}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{3}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知直线l:y=kx-2与抛物线C:x2=-2py(p>0)交于A,B两点,线段AB的中点坐标为(-2,-6).
如图,已知直线l:y=kx-2与抛物线C:x2=-2py(p>0)交于A,B两点,线段AB的中点坐标为(-2,-6).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知抛物线G的顶点在原点,焦点F为圆(x-1)2+y2=1的圆心.设过点F的直线与抛物线G及圆F依次交于如图中所示的A,B,C,D四点.
已知抛物线G的顶点在原点,焦点F为圆(x-1)2+y2=1的圆心.设过点F的直线与抛物线G及圆F依次交于如图中所示的A,B,C,D四点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在棱长为1正四面体S-ABC,O是四面体的中心,平面PQR∥平面ABC,设SP=x(0≤x≤1),三棱锥O-PQR的体积为V=f(x),其导函数y=f(x)的图象大致为( )
如图,在棱长为1正四面体S-ABC,O是四面体的中心,平面PQR∥平面ABC,设SP=x(0≤x≤1),三棱锥O-PQR的体积为V=f(x),其导函数y=f(x)的图象大致为( )| A. | 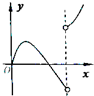 | B. |  | C. |  | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com