
���� ��������C�ļ����귽�̼� ��2=6��cos�ȣ����� x=��cos�ȣ�y=��sin�ȣ�������Ϊֱ�����귽�̣���ȥ�������ɵ�ֱ��l����ͨ���̣�
������ȷ��AC2+BD2Ϊ��ֵ����ʾ��������������ı���ABCD����������ֵ����Сֵ��
��� �⣺��������C�ļ����귽��Ϊ��=6cos�ȣ��� ��2=6��cos�ȣ���Ϊֱ�����귽��Ϊ x2+y2=6x��
ֱ��l�IJ���������$\left\{\begin{array}{l}x=4+tcos��\\ y=-1+tsin��\end{array}\right.$��tΪ�������ȡ�R����ֱ��l����ͨ����y+1=tan�ȣ�x-4����
��������AC��BD���е�ֱ�ΪE��F����OE2+OF2=2��
��AC2+BD2=4��18-OE2-OF2��=64��
��S2=$\frac{1}{4}$AC2•BD2=$\frac{1}{4}$AC2•��64-AC2����256��
��S��16�����ҽ���AC2=64-AC2����AC=4$\sqrt{2}$ʱ��ȡ�Ⱥţ�
���ı���ABCD���S�����ֵΪ16��
���� ������Ҫ����Ѽ����귽�̻�Ϊֱ�����귽�̵ķ������������̻�Ϊ��ͨ���̵ķ���������ֱ�߹����㣬��������ļ��㣬��������ʽ��Ӧ�ã���ȷ���ô��뷨�ǽ���Ĺؼ��������е��⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���������t����λ���棩 | t��22�� | 22�棼t��28�� | 28�棼t��32�� | t��32�� |
| ���� | 6 | 12 | X | Y |
| �������� | �Ǹ������� | �ϼ� | |
| ���� | 2 | 22 | 24 |
| ������ | 4 | 2 | 6 |
| �ϼ� | 6 | 24 | 30 |
| P��K2��k�� | 0.10 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | $\frac{3}{4}$ | C�� | 1 | D�� | $\frac{4}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
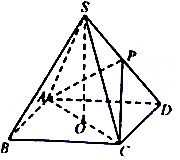 ��ͼ��������S-ABCD�У���O��������ABCD�����ģ�SO��ƽ��ABCD����SO=OD����PΪ��SD��һ�㣮
��ͼ��������S-ABCD�У���O��������ABCD�����ģ�SO��ƽ��ABCD����SO=OD����PΪ��SD��һ�㣮�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com