
| A. | (-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$) | B. | (-∞,-$\frac{\sqrt{3}}{3}$)∪($\frac{\sqrt{3}}{3}$,+∞) | C. | [-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$] | D. | (-$\frac{\sqrt{3}}{3}$,0)∪(0,$\frac{\sqrt{3}}{3}$) |
分析 把圆的方程化为标准方程,求出圆心和半径,直线过定点(-1,0),当直线y-mx-m=0与圆相切时,根据圆心到直线的距离d=$\frac{2|m|}{\sqrt{{m}^{2}+1}}$=r=1,求出m的值,数形结合求出实数m的取值范围.
解答 解:由题意可知曲线C1:x2+y2-2x=0表示一个圆,
化为标准方程得: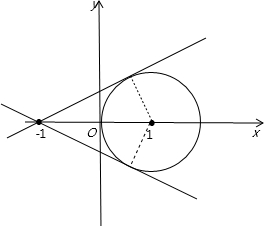 (x-1)2+y2=1,
(x-1)2+y2=1,
所以圆心坐标为(1,0),半径r=1;
C2:y(y-mx-m)=0表示两条直线y=0和y-mx-m=0,
由直线y-mx-m=0可知:此直线过定点(-1,0),
在平面直角坐标系中画出图象如图所示:
当直线y-mx-m=0与圆相切时,
圆心到直线的距离d=$\frac{2|m|}{\sqrt{{m}^{2}+1}}$=r=1,
化简得:m2=$\frac{1}{3}$,m=±$\frac{\sqrt{3}}{3}$.
则直线y-mx-m=0与圆相交时,
m∈(-$\frac{\sqrt{3}}{3}$,0)∪(0,$\frac{\sqrt{3}}{3}$),
故选:D.
点评 本题主要考查直线和圆的位置关系,点到直线的距离公式的应用,体现了数形结合的数学思想,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $({\frac{1}{3},+∞})$ | B. | $({\frac{2}{3},1})$ | C. | (2,+∞) | D. | $({\frac{3}{2},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -10 | B. | 10 | C. | -5 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | 4 | D. | $\frac{16}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
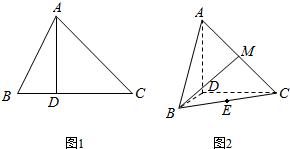 已知△ABC中,∠ACB=45°,B、C为定点且BC=3,A为动点,作AD⊥BC于D(异于点B),如图1所示.连接AB,将△ABD沿AD折起,使平面ABD⊥平面ADC,如图2所示.
已知△ABC中,∠ACB=45°,B、C为定点且BC=3,A为动点,作AD⊥BC于D(异于点B),如图1所示.连接AB,将△ABD沿AD折起,使平面ABD⊥平面ADC,如图2所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
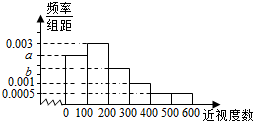 某普通高中为了了解学生的视力状况,随机抽查了100名高二年级学生和100名高三年级学生,对这些学生配戴眼镜的度数(简称:近视度数)进行统计,得到高二学生的频数分布表和高三学生频率分布直方图如下:
某普通高中为了了解学生的视力状况,随机抽查了100名高二年级学生和100名高三年级学生,对这些学生配戴眼镜的度数(简称:近视度数)进行统计,得到高二学生的频数分布表和高三学生频率分布直方图如下:| 近视度数 | 0-100 | 100-200 | 200-300 | 300-400 | 400以上 |
| 学生频数 | 30 | 40 | 20 | 10 | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com