
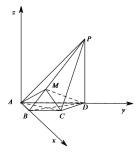
【题目】四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
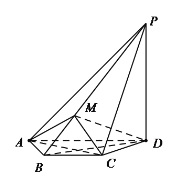
(1)求证: 平面![]() 平面
平面![]() ;
;
(2)![]() 为棱
为棱![]() 上异于
上异于![]() 的点,且
的点,且![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析(2)![]()
【解析】
(1)根据相似三角形,证得![]() ,又由
,又由![]() 平面
平面![]() ,得到
,得到![]()
![]() ,利用线面垂直的判定定理,证得
,利用线面垂直的判定定理,证得![]() 平面
平面![]() ,再由面面垂直的判定定理,即可得到平面
,再由面面垂直的判定定理,即可得到平面![]() 平面
平面![]() .
.
(2)以![]() 为原点,
为原点,![]() 所在的直线为
所在的直线为![]() 轴,建立空间直角坐标系,设
轴,建立空间直角坐标系,设![]() ,
,![]() ,利用以
,利用以![]() ,求得
,求得![]() ,得到
,得到![]() ,再求得平面
,再求得平面![]() 的一个法向量
的一个法向量![]() ,利用向量的夹角公式,即可求解.
,利用向量的夹角公式,即可求解.
(1)证明:在![]() 与
与![]() 中,因为
中,因为![]() ,
, ![]() ,
,
所以![]() ,
,![]() ,即
,即![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() ,所以
,所以![]() .
.
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]()
![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() , 所以平面
, 所以平面![]() 平面
平面![]() .
.

(2)过![]() 作
作![]() ,因为
,因为![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,即
,即![]() 两两相垂直,以
两两相垂直,以![]() 为原点,
为原点,![]() 所在的直线为
所在的直线为![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
因为![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
设![]() ,
,![]() .则
.则![]() ,
,
![]() .
.
因为![]() ,所以
,所以![]() ,即
,即![]() ,
,
解得![]() ,
,![]() 或
或![]() .因为
.因为![]() ,所以
,所以![]() .
.
所以![]() ,即
,即![]() .
.
设![]() 为平面
为平面![]() 的一个法向量,则
的一个法向量,则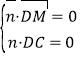 ,
,![]()
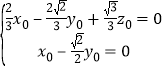
所以取![]() ,
,
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
![]()
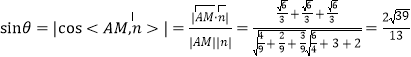 ,
,
所以直线![]() 与平面
与平面![]() 所成角的正弦值
所成角的正弦值![]() .
.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
【题目】若函数![]() 在区间
在区间![]() 上,
上, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 均可为一个三角形的三边长,则称函数
均可为一个三角形的三边长,则称函数![]() 为“三角形函数”.已知函数
为“三角形函数”.已知函数![]() 在区间
在区间![]() 上是“三角形函数”,则实数
上是“三角形函数”,则实数![]() 的取值范围为( )
的取值范围为( )
A.  B.
B. ![]()
C. ![]() D.
D. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:①![]() 越小,X与Y有关联的可信度越小;②若两个随机变量的线性相关性越强,则相关系数r的值越接近于1;③“若
越小,X与Y有关联的可信度越小;②若两个随机变量的线性相关性越强,则相关系数r的值越接近于1;③“若![]() ,则
,则![]() 类比推出,“若
类比推出,“若![]() ,则
,则![]() ;④命题“有些有理数是无限循环小数,整数是有理数,所以整数是无限循环小数”是假命题,推理错误的原因是使用了“三段论”,推理形式错误.其中说法正确的有( )个
;④命题“有些有理数是无限循环小数,整数是有理数,所以整数是无限循环小数”是假命题,推理错误的原因是使用了“三段论”,推理形式错误.其中说法正确的有( )个
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某新上市的电子产品举行为期一个星期(7天)的促销活动,规定购买该电子产品可免费赠送礼品一份,随着促销活动的有效开展,第五天工作人员对前五天中参加活动的人数进行统计,![]() 表示第
表示第![]() 天参加该活动的人数,得到统计表格如下:
天参加该活动的人数,得到统计表格如下:
| 1 | 2 | 3 | 4 | 5 |
| 4 | 6 | 10 | 23 | 22 |
(1)若![]() 与
与![]() 具有线性相关关系,请根据上表提供的数据,用最小二乘法求出
具有线性相关关系,请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)预测该星期最后一天参加该活动的人数(按四舍五入取到整数).
参考公式: ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面给出了根据我国2012年~2018年水果人均占有量y(单位:kg)和年份代码x绘制的散点图(2012年~2018年的年份代码x分别为1~7).

(1)根据散点图相应数据计算得![]() ,
,![]() ,求y关于x的线性回归方程;
,求y关于x的线性回归方程;
(2)估计我国2023年水果人均占有量是多少?(精确到1kg).
附:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com