练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】若函数在区间上， ， ， ， ， ， 均可为一个三角形的三边长，则称函数为“三角形函数”．已知函数在区间上是“三角形函数”，则实数的取值范围为（ ）

    A. B.

    C. D.

    【答案】D

    【解析】试题分析：根据“三角形函数”的定义可知，若在区间上的“三角形函数”，则在上的最大值和最小值应满足，由可得，所以在上单调递减，在上单调递增， ，所以，解得的取值范围为，故选A.

    【方法点睛】本题主要考查了利用导数研究函数在闭区间上的最值，考查考生应用所学知识解决问题的能力，属于中档题.解答本题首先通过给出的定义把问题转化为函数的最值问题，通过导数研究其单调性，得到最小值，通过比较区间端点的函数值求出最大值，列出关于参数的不等式，进而求得其范围.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设各项均为正数的数列满足（为常数），其中为数列的前项和.

    （1）若，，求证：是等差数列；

    （2）若，，求数列的通项公式；

    （3）若，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

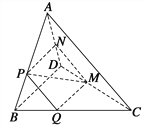
    【题目】如图，在四面体ABCD中，截面PQMN是正方形，则下列命题中，正确的为________ (填序号)．

    ①AC⊥BD；②AC∥截面PQMN；③AC＝BD；④异面直线PM与BD所成的角为45°.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆：（）的离心率为，右焦点为，斜率为1的直线与椭圆交于、两点，以为底边作等腰三角形，顶点为．

    （1）求椭圆的方程；

    （2）求△的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率为，点在椭圆上．

    （I）求椭圆的方程；

    （II）设动直线与椭圆有且仅有一个公共点，判断是否存在以原点为圆心的圆，满足此圆与相交于两点（两点均不在坐标轴上），且使得直线的斜率之积为定值？若存在，求此圆的方程；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆经过点，圆的圆心在圆的内部，且直线被圆所截得的弦长为.点为圆上异于的任意一点，直线与轴交于点，直线与轴交于点.

    （1）求圆的方程；

    （2）求证: 为定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

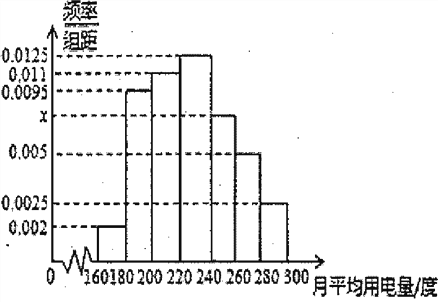
    【题目】某城市100户居民的月平均用电量（单位：度）以[160，180），[180，200），[200，220），[220，240），[240，260），[260，280），[280，300]分组的频率分布直方图如下图示．

    （Ⅰ）求直方图中x的值；

    （Ⅱ）求月平均用电量的众数和中位数；

    （Ⅲ）在月平均用电量为[220，240），[240，260），[260，280）的三组用户中，用分层抽样的方法抽取10户居民，则月平均用电量在[220，240）的用户中应抽取多少户？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）当时，求函数在区间上的最大值与最小值；

    （2）若在上存在，使得成立，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}是公差为3的等差数列，数列{bn}满足b1=1，b2=，anbn+1+bn+1=nbn．

    （Ⅰ）分别求数列{an}，{bn}的通项公式；

    （Ⅱ）令cn= an bn，求数列{cn}的前n项和Tn．

    查看答案和解析>>

    同步练习册答案