
分析 (1)利用an+1=Sn+1-Sn,结合已知条件,推出数列{Sn}是首项为1,公比为3的等比数列,求出Sn,然后求解通项公式.
(2)利用错位相减法,求解数列的和即可.
解答 解:(1)∵an+1=2Sn,
∴Sn+1-Sn=2Sn,
∴$\frac{{S}_{n+1}}{{S}_{n}}$=3,
又∵S1=a1=1,
∴数列{Sn}是首项为1,公比为3的等比数列,Sn=3n-1(n∈N*).
∴当n≥2时,an=2Sn-1=2•3n-2(n≥2),
∴an=$\left\{\begin{array}{l}{1,n=1}\\{2•{3}^{n-2},n≥2}\end{array}\right.$;
(2)Tn=a1+2a2+3a3+…+nan,
当n=1时,T1=1;
当n≥2时,Tn=1+4•30+6•31+2n•3n-2,…①
3Tn=3+4•31+6•32+…+2n•3n-1,…②
①-②得:-2Tn=-2+4+2(31+32+…+3n-2)-2n•3n-1
=2+2•$\frac{3(1-{3}^{n-2})}{1-3}$-2n•3n-1=-1+(1-2n)•3n-1,
∴Tn=$\frac{1}{2}$+(n-$\frac{1}{2}$)3n-1(n≥2),
又∵T1=a1=1也满足上式,
∴Tn=$\frac{1}{2}$+(n-$\frac{1}{2}$)3n-1(n∈N*).
点评 本题考查数列的递推关系式的应用,等比数列的判断,数列求和的方法,考查转化思想以及计算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若“p且q”为假命题,则p、q均为假命题 | |
| B. | 命题“若a>b,则2a>2b-1”的否命题为“若a≤b,则2a≤2b-1” | |
| C. | “?x∈R,x2+1≥1”的否定是“?x∈R,x2+1≤1” | |
| D. | 在△ABC中,“A>B”是“sinA>sinB”的充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)+g(x) 为减函数 | B. | f(x)-g(x)为增函数 | C. | f(x)•g(x)是减函数 | D. | $\frac{f(x)}{g(x)}$ 是增函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
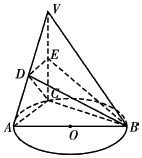 如图AB是圆O的直径,点C是弧AB上一点,VC垂直圆O所在平面,D,E分别为VA,VC的中点.
如图AB是圆O的直径,点C是弧AB上一点,VC垂直圆O所在平面,D,E分别为VA,VC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $a+\frac{1}{b}>b+\frac{1}{a}$ | B. | $\frac{b}{a}>\frac{b+1}{a+1}$ | C. | $a-\frac{1}{b}>b-\frac{1}{a}$ | D. | $\frac{2a+b}{a+2b}>\frac{a}{b}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com