Question

1．已知关于x的一元二次方程x²-2（a-2）-b²+16=0．
（1）若a、b是一枚骰子掷两次所得到的点数，求方程有两正根的概率；
（2）若a∈[2，4]，b∈[0，6]，求方程没有实根的概率．

Answer 1

分析 （1）本题是一个古典概型，用（a，b）表示一枚骰子投掷两次所得到的点数的事件，基本事件（a，b）的总数有36个满足条件的事件是二次方程x²-2（a-2）x-b²+16=0有两正根，根据实根分布得到关系式，得到概率．
（2）本题是一个几何概型，试验的全部结果构成区域Ω={（a，b）|2≤a≤4，0≤b≤6}，满足条件的事件为：B={（a，b）|2≤a≤4，0≤b≤6，（a-2）²+b²＜16}，做出两者的面积，得到概率．

解答 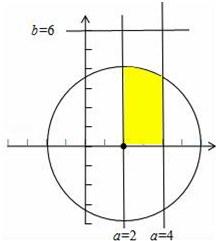解：设“方程有两个正根”的事件为A，
（1）由题意知本题是一个古典概型用（a，b）表示一枚骰子投掷两次所得到的点数的事件
依题意知，基本事件（a，b）的总数有36个，
二次方程x²-2（a-2）x-b²+16=0有两正根，等价于$\left\{\begin{array}{l}{a-2＞0}\\{16-{b}^{2}＞0}\\{4（a-2）^{2}+4（{b}^{2}-16）≥0}\end{array}\right.$
即$\left\{\begin{array}{l}{a＞2}\\{-4＜b＜4}\\{（a-2）^{2}+{b}^{2}≥16}\end{array}\right.$，
则事件A包含的基本事件为（6，1）、（6，2）、（6，3）、（5，3）共4个
∴所求的概率为P（A）=$\frac{1}{9}$；
（2）由题意知本题是一个几何概型，
试验的全部结果构成区域Ω={（a，b）|2≤a≤4，0≤b≤6}，
其面积为S（Ω）=12
满足条件的事件为：B={（a，b）|2≤a≤4，0≤b≤6，（a-2）²+b²＜16}，如图中阴影部分所示，
其面积为S（B）=$\frac{1}{2}×\frac{π}{6}×4×4+\frac{1}{2}×2×\sqrt{16-4}$=$\frac{4π}{3}+2\sqrt{3}$，
∴所求的概率P（B）=$\frac{2π+3\sqrt{3}}{18}$．

点评 本题考查古典概型和几何概型，几何概型和古典概型是高中必修中学习的，高考时常以选择和填空出现，有时文科会考这种类型的解答题目．