
| A. | 1<e≤2 | B. | e≥2 | C. | 1<e≤$\sqrt{2}$ | D. | e≥$\sqrt{2}$ |
分析 利用向量平行四边形法则可得:$\overrightarrow{PA}+\overrightarrow{PB}$=$2\overrightarrow{PO}$,又$|\overrightarrow{PO}|$≥a,根据双曲线上存在点P满足2|$\overrightarrow{PA}$+$\overrightarrow{PB}$|≤|$\overrightarrow{AB}$|,代入即可得出.
解答 解:∵$\overrightarrow{PA}+\overrightarrow{PB}$=$2\overrightarrow{PO}$,在双曲线上存在点P满足2|$\overrightarrow{PA}$+$\overrightarrow{PB}$|≤|$\overrightarrow{AB}$|,
∴$4|\overrightarrow{PO}|$≤2c,又$|\overrightarrow{PO}|$≥a,
∴2a≤c,解得e≥2.
故选:B.
点评 本题考查了双曲线的标准方程及其性质、向量平行四边形法则,考查了推理能力与计算能力,属于中档题.


 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{4}{27}$ | B. | -$\frac{2}{27}$ | C. | $\frac{2}{27}$ | D. | $\frac{4}{27}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)+g(x) 为减函数 | B. | f(x)-g(x)为增函数 | C. | f(x)•g(x)是减函数 | D. | $\frac{f(x)}{g(x)}$ 是增函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
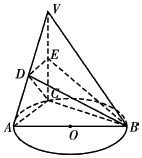 如图AB是圆O的直径,点C是弧AB上一点,VC垂直圆O所在平面,D,E分别为VA,VC的中点.
如图AB是圆O的直径,点C是弧AB上一点,VC垂直圆O所在平面,D,E分别为VA,VC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com