
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)讨论函数![]() 的零点个数.
的零点个数.
【答案】(1)当![]() 时,
时,![]() 在
在![]() 上单调递增,当
上单调递增,当![]() 时,
时,![]() 在
在![]() )上单调递减,在
)上单调递减,在![]() 上单调递增;(2)当
上单调递增;(2)当![]() 或
或![]() 时,
时,![]() 有1个零点;当
有1个零点;当![]() 时,
时,![]() 有2个零点;当
有2个零点;当![]() 时,
时,![]() 有0个零点.
有0个零点.
【解析】
(1)对函数![]() 求导,分类讨论
求导,分类讨论![]() 和
和![]() 时的单调性,即可得到结果.
时的单调性,即可得到结果.
(2)![]() 不是
不是![]() 的零点,即可分类参量,求解
的零点,即可分类参量,求解![]() 的交点个数问题,对新函数
的交点个数问题,对新函数![]() 求导后作图,进而计算出零点个数问题.
求导后作图,进而计算出零点个数问题.
(1)![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
当![]() 时,
时,![]() 所以
所以![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时,由
时,由![]() 得
得![]() ,
,
所以![]() ,
,![]() ,
,![]() 单调递减,
单调递减,
![]() ,
,![]() ,
,![]() 单调递增 ,
单调递增 ,
综上,当![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时,
时,![]() 在
在![]() )上单调递减,在
)上单调递减,在![]() 上单调递增;
上单调递增;
(2)显然![]() 不是
不是![]() 的零点,
的零点,
当![]() 时,由
时,由![]() 得
得![]() ,
,
令![]() ,则
,则![]() .
.
所以![]() 在
在![]() 上单调递减,
上单调递减,![]() 上单调递减,
上单调递减,![]() 上单调递增,
上单调递增,
且当![]() 时,
时,![]() ,当x从左边趋近于0时,
,当x从左边趋近于0时,![]() ,当x从右边趋近于0时,
,当x从右边趋近于0时,![]() ,画出
,画出![]() 的图象如图,数形结合知,
的图象如图,数形结合知,
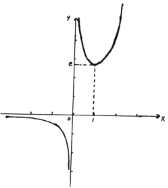
当![]() 或
或![]() 即
即![]() 或
或![]() 时,
时,![]() 有1个零点,
有1个零点,
当![]() 即
即![]() 时,
时,![]() 有2个零点,
有2个零点,
当![]() 即
即![]() 时,
时,![]() 有0个零点.
有0个零点.


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.![]() 为曲线
为曲线![]() 上的动点,点
上的动点,点![]() 在射线
在射线![]() 上,且满足
上,且满足![]() .
.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设![]() 与
与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 且倾斜角为
且倾斜角为![]() 的直线
的直线![]() 与
与![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将420名工人编号为:001,002,![]() ,420,采用系统抽样的方法抽取一个容量为60的样本,且随机抽得的号码为005.这420名工人来自三个工厂,从001到200为
,420,采用系统抽样的方法抽取一个容量为60的样本,且随机抽得的号码为005.这420名工人来自三个工厂,从001到200为![]() 工厂,从201到355为
工厂,从201到355为![]() 工厂,从356到420为
工厂,从356到420为![]() 工厂,则三个工厂被抽中的工人数依次为( )
工厂,则三个工厂被抽中的工人数依次为( )
A.28,23,9B.27,23,10C.27,22,11D.28,22,10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现在给出三个条件:①a=2;②B![]() ;③c
;③c![]() b.试从中选出两个条件,补充在下面的问题中,使其能够确定△ABC,并以此为依据,求△ABC的面积.
b.试从中选出两个条件,补充在下面的问题中,使其能够确定△ABC,并以此为依据,求△ABC的面积.
在△ABC中,a、b、c分别是角A、B、C的对边,且满足![]() ,求△ABC的面积(选出一种可行的方案解答,若选出多个方案分别解答,则按第一个解答记分)
,求△ABC的面积(选出一种可行的方案解答,若选出多个方案分别解答,则按第一个解答记分)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,直线l:![]() ,P为直线l上一点,且点P在极轴上方
,P为直线l上一点,且点P在极轴上方![]() 以OP为一边作正三角形
以OP为一边作正三角形![]() 逆时针方向
逆时针方向![]() ,且
,且![]() 面积为
面积为![]() .
.
![]() 求Q点的极坐标;
求Q点的极坐标;
![]() 求
求![]() 外接圆的极坐标方程,并判断直线l与
外接圆的极坐标方程,并判断直线l与![]() 外接圆的位置关系.
外接圆的位置关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地举办水果观光采摘节,并推出配套旅游项目,统计了4月份100名游客购买水果的情况,得到如图所示的频率分布直方图.
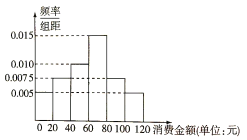
(1)若将消费金额不低于80元的游客称为“水果达人”,现用分层抽样的方法从样本的“水果达人”中抽取5人,求这5人中消费金额不低于100元的人数;
(2)从(1)中的5人中抽取2人作为幸运客户免费参加配套旅游项目,请列出所有的可能结果,并求这2人中至少有1人购买金额不低于100元的概率;
(3)为吸引顾客,该地特推出两种促销方案,
方案一:每满80元可立减8元;
方案二:金额超过50元但又不超过80元的部分打9折,金额超过80元但又不超过100元的部分打8折,金额超过100元的部分打7折.
若水果的价格为11元/千克,某游客要购买10千克,应该选择哪种方案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的方程为
的方程为![]() ,
,![]() 是椭圆上的一点,且
是椭圆上的一点,且![]() 在第一象限内,过
在第一象限内,过![]() 且斜率等于-1的直线与椭圆
且斜率等于-1的直线与椭圆![]() 交于另一点
交于另一点![]() ,点
,点![]() 关于原点的对称点为
关于原点的对称点为![]() .
.
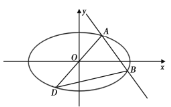
(1)证明:直线![]() 的斜率为定值;
的斜率为定值;
(2)求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为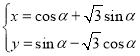 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,取相同长度单位建立极坐标系,直线
轴的正半轴为极轴,取相同长度单位建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 和直线
和直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)直线![]() 与
与![]() 轴交点为
轴交点为![]() ,经过点
,经过点![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() ,
,![]() 两点,证明:
两点,证明:![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com