
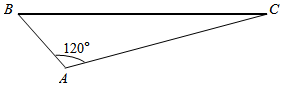
 �����к����̻�������չ���̻���ҵ�Ǵٽ����Ҿ��÷�չ�ͳ��н�����ҵ����Ҫ��ɲ��֣�ij������Ӧ�����̻��ĺ��٣��ƻ���һ��ͼ��ʾ��������ABC��״�����������һ�������ֳɵ�ΧǽBC������Ϊ100$\sqrt{3}$�ף���������AB��ACʹ��ij�����Ͳ���Χ�ɣ���֪��BAC=120�㣬AB=x��AC=y��x��y��λ��Ϊ�ף���
�����к����̻�������չ���̻���ҵ�Ǵٽ����Ҿ��÷�չ�ͳ��н�����ҵ����Ҫ��ɲ��֣�ij������Ӧ�����̻��ĺ��٣��ƻ���һ��ͼ��ʾ��������ABC��״�����������һ�������ֳɵ�ΧǽBC������Ϊ100$\sqrt{3}$�ף���������AB��ACʹ��ij�����Ͳ���Χ�ɣ���֪��BAC=120�㣬AB=x��AC=y��x��y��λ��Ϊ�ף������� ��1���������⣬�����Ҷ����ɵ�x2+y2-2xycos120��=30000�����οɵ�x2+y2+xy=30000������x��y��ȡֵ��Χ���ɵô𰸣�
��2���ɣ�1���ɵ�x2+y2+xy=30000��������οɵ�x2+y2+xy=30000��3xy���Ӷ��õ���������������ֵ��
��� �⣺��1���ڡ�ABC�У������Ҷ�������AB2+AC2-2AB•ACcosA=BC2��
����x2+y2-2xycos120��=30000��
��x2+y2+xy=30000������4�֣�
����Ϊx��0��y��0������0��x��100$\sqrt{3}$��0��y��100$\sqrt{3}$������6�֣�
��2���ɣ�1��x2+y2+xy=30000��30000��2xy+xy=3xy������xy��1000��
Ҫʹ�������ʹ����������S=$\frac{1}{2}xysin120��$�������S=$\frac{\sqrt{3}}{4}xy��\frac{\sqrt{3}}{4}��10000=2500\sqrt{3}$��
���ҽ���x=y=100ʱ����ʽ����ʽ����������11�֣�
�ʵ�AB��AC�߳���Ϊ100��ʱ���������ʹ�������������Ϊ2500$\sqrt{3}$��2��
���� ���⿼���������ʽ����ֵ�����е����ã��ؼ����������Ҷ����õ�����x��y֮��Ĺ�ϵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | $\frac{1}{3}$ | C�� | -3 | D�� | -2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{6}$ | B�� | $\frac{1}{4}$ | C�� | $\frac{1}{3}$ | D�� | $\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | A${\;}_{18}^{12}$ | B�� | A${\;}_{18}^{6}$ | C�� | A${\;}_{18}^{7}$ | D�� | A${\;}_{18}^{11}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com