
 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:解答题
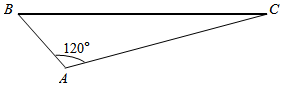 “城市呼唤绿化”,发展园林绿化事业是促进国家经济发展和城市建设事业的重要组成部分,某城市响应城市绿化的号召,计划建一如图所示的三角形ABC形状的主题公园,其中一边利用现成的围墙BC,长度为100$\sqrt{3}$米,另外两边AB,AC使用某种新型材料围成,已知∠BAC=120°,AB=x,AC=y(x,y单位均为米).
“城市呼唤绿化”,发展园林绿化事业是促进国家经济发展和城市建设事业的重要组成部分,某城市响应城市绿化的号召,计划建一如图所示的三角形ABC形状的主题公园,其中一边利用现成的围墙BC,长度为100$\sqrt{3}$米,另外两边AB,AC使用某种新型材料围成,已知∠BAC=120°,AB=x,AC=y(x,y单位均为米).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com