Question

5．已知二次函数f（x）=x²+bx+c（b，c∈R）．
（Ⅰ）若f（-2）=f（2），f（1）≥0，且不等式f（x）≤|x-1|对所有x∈[0，1]都成立，求函数f（x）的解析式；
（Ⅱ）若c＜0，且函数f（x）在[-1，1]上有两个零点，求b+2c的取值范围；
（Ⅲ）在（Ⅰ）的条件下，当$x≥\frac{3}{2}$时，都有$f（x-1）+4{a^2}f（x）≥f（\frac{x}{a}）-4f（a）$成立，求证：关于x的方程16x²-16ax+3=0有实根．

Answer 1

分析 （Ⅰ）由f（-2）=f（2）得到b=0，求出f（x）=x²+c，而f（1）≥0，所以1+c≥0，当x∈[0，1]时，由f（x）≤|x-1|得x²+c≤1-x，即x²+x+c-1≤0，令y=x²+x+c-1要使f（x）≤|x-1|对所有x∈[0，1]都成立，只需y_max≤0，而$y={（x+\frac{1}{2}）^2}+c-\frac{5}{4}$，且函数y在[0，1]上单调递增，求出y的最大值可得到1+c≤0，于是0≤1+c≤0即1+c=0，即可求出函数f（x）的解析式；
（Ⅱ）由题意知$\left\{{\begin{array}{l}{f（-1）≥0}\\{f（1）≥0}\\{c＜0}\end{array}}\right.$进一步得到$\left\{{\begin{array}{l}{1-b+c≥0}\\{1+b+c≥0}\\{c＜0}\end{array}}\right.$，令z=b+2c，画出可行域，由线性规划知识可得b+2c的取值范围；
（Ⅲ）由（Ⅰ）知，f（x）=x²-1，再根据$f（x-1）+4{a^2}f（x）≥f（\frac{x}{a}）-4f（a）$得到${（x-1）^2}-1+4{a^2}（{x^2}-1）≥{（\frac{x}{a}）^2}-1-4（{a^2}-1）$，进一步化简得$4{a^2}-\frac{1}{a^2}≥\frac{{-{x^2}+2x+3}}{x^2}=3\frac{1}{x^2}+2\frac{1}{x}-1$，要使$x≥\frac{3}{2}$时，都有$f（x-1）+4{a^2}f（x）≥f（\frac{x}{a}）-4f（a）$成立，只需$4{a^2}-\frac{1}{a^2}≥{（{3\frac{1}{x^2}+2\frac{1}{x}-1}）_{max}}$（$x≥\frac{3}{2}$），令$y=3\frac{1}{x^2}+2\frac{1}{x}-1$（$0＜\frac{1}{x}≤\frac{2}{3}$）配方得$y=3{（{\frac{1}{x}+\frac{1}{3}}）^2}-\frac{4}{3}$，当$0＜\frac{1}{x}≤\frac{2}{3}$时函数y单调递增，可求出y的最大值，因此$4{a^2}-\frac{1}{a^2}≥\frac{5}{3}$，化简求出${a^2}≥\frac{3}{4}$，而在方程16x²-16ax+3=0中，△=64•（4a²-3）≥0，即可证明关于x的方程16x²-16ax+3=0有实数根．

解答 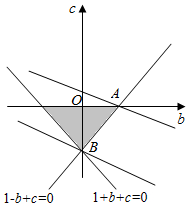（Ⅰ）解：∵f（-2）=f（2），∴b=0．
∴f（x）=x²+c…（1分）
而f（1）≥0，∴1+c≥0．
当x∈[0，1]时，由f（x）≤|x-1|得x²+c≤1-x，即x²+x+c-1≤0．
令y=x²+x+c-1要使f（x）≤|x-1|对所有x∈[0，1]都成立，
只需y_max≤0，而$y={（x+\frac{1}{2}）^2}+c-\frac{5}{4}$，且函数y在[0，1]上单调递增，
∴${y_{max}}={1^2}+1+c-1=c+1$，故1+c≤0．
于是0≤1+c≤0即1+c=0，∴c=-1．
∴f（x）=x²-1…（3分）
（Ⅱ）解：由题意知$\left\{{\begin{array}{l}{f（-1）≥0}\\{f（1）≥0}\\{c＜0}\end{array}}\right.$，∴$\left\{{\begin{array}{l}{1-b+c≥0}\\{1+b+c≥0}\\{c＜0}\end{array}}\right.$…（6分）
令z=b+2c，画出可行域，
由z=b+2c，得$c=-\frac{b}{2}+\frac{z}{2}$，
由线性规划知识可知-2≤b+2c＜1…（8分）
（Ⅲ）证明：由（Ⅰ）知，f（x）=x²-1，
∵$f（x-1）+4{a^2}f（x）≥f（\frac{x}{a}）-4f（a）$，
∴${（x-1）^2}-1+4{a^2}（{x^2}-1）≥{（\frac{x}{a}）^2}-1-4（{a^2}-1）$，
∴$4{a^2}-\frac{1}{a^2}≥\frac{{-{x^2}+2x+3}}{x^2}=3\frac{1}{x^2}+2\frac{1}{x}-1$．
要使$x≥\frac{3}{2}$时，都有$f（x-1）+4{a^2}f（x）≥f（\frac{x}{a}）-4f（a）$成立，只需$4{a^2}-\frac{1}{a^2}≥{（{3\frac{1}{x^2}+2\frac{1}{x}-1}）_{max}}$（$x≥\frac{3}{2}$）…（10分）
令$y=3\frac{1}{x^2}+2\frac{1}{x}-1$（$0＜\frac{1}{x}≤\frac{2}{3}$）
配方得$y=3{（{\frac{1}{x}+\frac{1}{3}}）^2}-\frac{4}{3}$，当$0＜\frac{1}{x}≤\frac{2}{3}$时函数y单调递增，
故y_max=$3{（{\frac{2}{3}+\frac{1}{3}}）^2}-\frac{4}{3}=\frac{5}{3}$，因此$4{a^2}-\frac{1}{a^2}≥\frac{5}{3}$，
∴12a⁴-5a²-3≥0，即（4a²-3）（3a²+1）≥0．
∴${a^2}≥\frac{3}{4}$或${a^2}≤-\frac{1}{3}$（舍）∴${a^2}≥\frac{3}{4}$…（11分）
而在方程16x²-16ax+3=0中，△=64•（4a²-3）≥0
∴关于x的方程16x²-16ax+3=0有实数根 …（12分）

点评 本题考查了二次函数的性质，考查了函数的单调性，考查了大量的计算能力，是有一定难度的题目．