
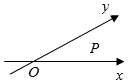
 如图,当∠xOy=α,且α∈(0,$\frac{π}{2}$)∪($\frac{π}{2}$,π)时,定义平面坐标系xOy为α-仿射坐标系.在α-仿射坐标系中,任意一点P的斜坐标这样定义:$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$分别为与x轴、y轴正向相同的单位向量,若$\overrightarrow{OP}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$,则记为$\overrightarrow{OP}$=(x,y).现给出以下说法:
如图,当∠xOy=α,且α∈(0,$\frac{π}{2}$)∪($\frac{π}{2}$,π)时,定义平面坐标系xOy为α-仿射坐标系.在α-仿射坐标系中,任意一点P的斜坐标这样定义:$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$分别为与x轴、y轴正向相同的单位向量,若$\overrightarrow{OP}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$,则记为$\overrightarrow{OP}$=(x,y).现给出以下说法:分析 把新定义回归到向量的数量积的运算对每个结论进行验证,即可得出结论.
解答 解:①在α-仿射坐标系中,已知$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(3,t),若$\overrightarrow{a}$∥$\overrightarrow{b}$,则1×t=2×3,∴t=6,正确;
②在α-仿射坐标系中,若$\overrightarrow{OP}$=($\frac{1}{2}$,$\frac{1}{3}$),若$\overrightarrow{OQ}$=($\frac{1}{3}$,-$\frac{1}{2}$),则$\overrightarrow{OP}$•$\overrightarrow{OQ}$=($\frac{1}{2}$$\overrightarrow{{e}_{1}}$+$\frac{1}{3}$$\overrightarrow{{e}_{2}}$)•($\frac{1}{3}$$\overrightarrow{{e}_{1}}$-$\frac{1}{2}$$\overrightarrow{{e}_{2}}$)=$\frac{1}{6}$-$\frac{5}{36}•1•1•cosα$-$\frac{1}{6}$≠0,故不正确;
③在60°-仿射坐标系中,若P(2,-1),则|$\overrightarrow{OP}$|=$\sqrt{4+1-2×2×1×\frac{1}{2}}$=$\sqrt{3}$,正确;
故答案为:①③.
点评 本题为新定义,正确理解题中给出的斜坐标并与已知的向量知识相联系是解决问题的关键,属基础题


科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{25}$ | B. | -$\frac{7}{25}$ | C. | 1 | D. | $\frac{\sqrt{7}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
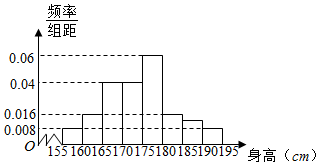 从某校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组,第一组[155,160),第二组[160,165),…,第八组[190.195],如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组人数为4.
从某校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组,第一组[155,160),第二组[160,165),…,第八组[190.195],如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组人数为4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | -2 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 0 | 1 | 2 | 3 |
| y | 1 | 3 | 5 | 7 |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若该大学某女生身高为170cm,则她的体重必为58.79kg | |
| B. | y与x具有正的线性相关关系 | |
| C. | 回归直线过样本点的中心($\overline x$,$\overline y$) | |
| D. | 身高x为解释变量,体重y为预报变量 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com