
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
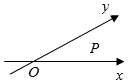 如图,当∠xOy=α,且α∈(0,$\frac{π}{2}$)∪($\frac{π}{2}$,π)时,定义平面坐标系xOy为α-仿射坐标系.在α-仿射坐标系中,任意一点P的斜坐标这样定义:$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$分别为与x轴、y轴正向相同的单位向量,若$\overrightarrow{OP}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$,则记为$\overrightarrow{OP}$=(x,y).现给出以下说法:
如图,当∠xOy=α,且α∈(0,$\frac{π}{2}$)∪($\frac{π}{2}$,π)时,定义平面坐标系xOy为α-仿射坐标系.在α-仿射坐标系中,任意一点P的斜坐标这样定义:$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$分别为与x轴、y轴正向相同的单位向量,若$\overrightarrow{OP}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$,则记为$\overrightarrow{OP}$=(x,y).现给出以下说法:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}+\sqrt{6}}{2}$ | B. | $\frac{\sqrt{2}-\sqrt{6}}{2}$ | C. | $\frac{\sqrt{2}+\sqrt{6}}{4}$ | D. | $\frac{\sqrt{2}-\sqrt{6}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “若$\overrightarrow a=\overrightarrow b$,则$|\overrightarrow a|=|\overrightarrow b|$”的逆命题 | B. | 命题“?x∈R,$x+\frac{1}{x}<2$”的否定 | ||
| C. | “面积相等的三角形全等”的否命题 | D. | “若A∩B=B,则A⊆B”的逆否命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
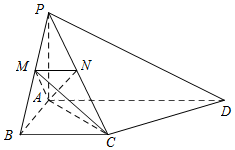 如图,PA⊥平面ABCD,AB⊥AD,AD∥BC,PA=AB=BC,AD=2AB,点M,N分别在PB,PC上,且MN∥BC.
如图,PA⊥平面ABCD,AB⊥AD,AD∥BC,PA=AB=BC,AD=2AB,点M,N分别在PB,PC上,且MN∥BC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com