
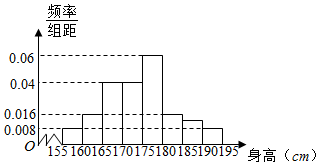
 ��ijУ��800�������������ȡ50���������ߣ�����ѧ������ȫ������155cm��195cm֮�䣬��������������·�ʽ�ֳɰ��飬��һ��[155��160�����ڶ���[160��165���������ڰ���[190.195]����ͼ�ǰ��������鷽���õ���Ƶ�ʷֲ�ֱ��ͼ��һ���֣���֪��һ����ڰ���������ͬ������������Ϊ4��
��ijУ��800�������������ȡ50���������ߣ�����ѧ������ȫ������155cm��195cm֮�䣬��������������·�ʽ�ֳɰ��飬��һ��[155��160�����ڶ���[160��165���������ڰ���[190.195]����ͼ�ǰ��������鷽���õ���Ƶ�ʷֲ�ֱ��ͼ��һ���֣���֪��һ����ڰ���������ͬ������������Ϊ4������ ��1���������⣬����������Ƶ�ʣ������Ӧ��Ƶ����
��2����λ������Ƶ����ȣ����ɵó���λ���ڵ����飻
����������180cm���ϵ�Ƶ�ʣ����800��ѧ����������180cm���ϣ���180cm����������
��� �⣺��1���������⣬�������Ƶ��Ϊ$\frac{4}{50}$=0.08��
�������Ƶ��Ϊ��1-��0.008��2+0.016+0.04��2+0.06����5-0.08=0.06��
��������Ƶ��Ϊ0.06��50=3��
��2���ɸ���Ƶ�ʿɵ��������ݣ�
| ��� | һ | �� | �� | �� | �� | �� | �� | �� |
| Ƶ�� | 0.04 | 0.08 | 0.20 | 0.20 | 0.30 | 0.08 | 0.06 | 0.04 |
���� ���⿼����Ƶ�ʷֲ�ֱ��ͼ��Ӧ�����⣬Ҳ������Ƶ�ʡ�Ƶ�������������Ĺ�ϵ���ǻ�����Ŀ��


 ��Ȥ����¹�֪��ϵ�д�
��Ȥ����¹�֪��ϵ�д� Ӣ��СӢ������Ĭдϵ�д�
Ӣ��СӢ������Ĭдϵ�д� �����ҵ���������ͯ������ϵ�д�
�����ҵ���������ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
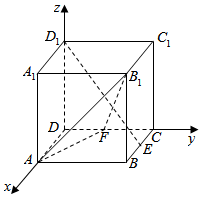 ���ⳤΪ1��������ABCDA1B1C1D1�У�EΪ��BC���е㣬��F����CD�ϵĶ��㣬��ȷ����F��λ�ã�ʹ��D1E��ƽ��AB1F��
���ⳤΪ1��������ABCDA1B1C1D1�У�EΪ��BC���е㣬��F����CD�ϵĶ��㣬��ȷ����F��λ�ã�ʹ��D1E��ƽ��AB1F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{6}$ | B�� | $\frac{1}{4}$ | C�� | $\frac{1}{3}$ | D�� | $\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���m?����n?����m��n������ֱ�ߣ���ôn�Φ� | |
| B�� | ���m?����n?����m��n������ֱ�ߣ���ôn����ཻ | |
| C�� | ���m?����n�Φ���m��n���棬��ôm��n | |
| D�� | ���m?����n��m����ôn�Φ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
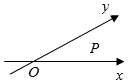 ��ͼ������xOy=�����Ҧ��ʣ�0��$\frac{��}{2}$���ȣ�$\frac{��}{2}$���У�ʱ������ƽ������ϵxOyΪ��-��������ϵ���ڦ�-��������ϵ�У�����һ��P��б�����������壺$\overrightarrow{{e}_{1}}$��$\overrightarrow{{e}_{2}}$�ֱ�Ϊ��x�ᡢy��������ͬ�ĵ�λ��������$\overrightarrow{OP}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$�����Ϊ$\overrightarrow{OP}$=��x��y�����ָ�������˵����
��ͼ������xOy=�����Ҧ��ʣ�0��$\frac{��}{2}$���ȣ�$\frac{��}{2}$���У�ʱ������ƽ������ϵxOyΪ��-��������ϵ���ڦ�-��������ϵ�У�����һ��P��б�����������壺$\overrightarrow{{e}_{1}}$��$\overrightarrow{{e}_{2}}$�ֱ�Ϊ��x�ᡢy��������ͬ�ĵ�λ��������$\overrightarrow{OP}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$�����Ϊ$\overrightarrow{OP}$=��x��y�����ָ�������˵�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����$\overrightarrow a=\overrightarrow b$����$|\overrightarrow a|=|\overrightarrow b|$���������� | B�� | ���⡰?x��R��$x+\frac{1}{x}��2$���ķ� | ||
| C�� | �������ȵ�������ȫ�ȡ��ķ����� | D�� | ����A��B=B����A⊆B����������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{{2}^{k}+1}$ | B�� | $\frac{1}{{2}^{k+1}}$ | ||
| C�� | $\frac{1}{{2}^{k}+1}$+$\frac{1}{{2}^{k}+2}$+��+$\frac{1}{{2}^{k+1}}$ | D�� | $\frac{1}{{2}^{k}}$+$\frac{1}{{2}^{k}+1}$+��+$\frac{1}{{2}^{k+1}}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com