
| A. | $\frac{1}{{2}^{k}+1}$ | B. | $\frac{1}{{2}^{k+1}}$ | ||
| C. | $\frac{1}{{2}^{k}+1}$+$\frac{1}{{2}^{k}+2}$+…+$\frac{1}{{2}^{k+1}}$ | D. | $\frac{1}{{2}^{k}}$+$\frac{1}{{2}^{k}+1}$+…+$\frac{1}{{2}^{k+1}}$ |
分析 求出当n=k时,左边的代数式,当n=k+1时,左边的代数式,相减可得结果.
解答 解:当n=k时,左边的代数式为$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+…+$\frac{1}{{2}^{K}}$
当n=k+1时,左边的代数式为$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+…+$\frac{1}{{2}^{K}}$+$\frac{1}{{2}^{k}+1}$+$\frac{1}{{2}^{k}+2}$+…+$\frac{1}{{2}^{k+1}}$,
故用n=k+1时左边的代数式减去n=k时左边的代数式的结果为$\frac{1}{{2}^{k}+1}$+$\frac{1}{{2}^{k}+2}$+…+$\frac{1}{{2}^{k+1}}$,
故选:C.
点评 本题考查用数学归纳法证明不等式,注意式子的结构特征,以及从n=k到n=k+1项的变化.


科目:高中数学 来源: 题型:解答题
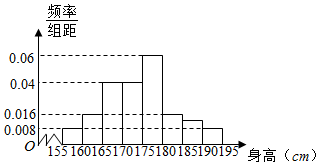 从某校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组,第一组[155,160),第二组[160,165),…,第八组[190.195],如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组人数为4.
从某校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组,第一组[155,160),第二组[160,165),…,第八组[190.195],如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组人数为4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若该大学某女生身高为170cm,则她的体重必为58.79kg | |
| B. | y与x具有正的线性相关关系 | |
| C. | 回归直线过样本点的中心($\overline x$,$\overline y$) | |
| D. | 身高x为解释变量,体重y为预报变量 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+2 | B. | 1+2+3+4 | C. | 1+2+3 | D. | 1+2+3+4+5+6+7+8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com