
分析 (Ⅰ)不妨设A(t,aln(t+2)),B(-t,t2),利用OA⊥OB,再分离参数,即可求a的取值集合;
(Ⅱ)函数g(x)=f1(x)+f2(x)存在两个极值点x1、x2,g′(x)=0,即2x2+4x+a=0在(-2,+∞)上存在两个不等的实根,可得0<a<2,x1+x2=-2,x1x2=$\frac{a}{2}$,表示出g(x1)+g(x2),确定其单调性,即可证明g(x1)+g(x2)>2.
解答 解:(Ⅰ)由题意,不妨设A(t,aln(t+2)),B(-t,t2)(t>0)
∴OA⊥OB,
∴-t2+at2ln(t+2)=0,
∴a=$\frac{1}{ln(t+2)}$,
∵ln(t+2)∈(ln2,+∞),
∴a的取值集合为(0,$\frac{1}{ln2}$);
(Ⅱ)g(x)=f1(x)+f2(x)=x2+aln(x+2),
∴g′(x)=$\frac{{2x}^{2}+4x+a}{x+2}$,
∵函数g(x)存在两个极值点x1、x2,
∴g′(x)=0,即2x2+4x+a=0在(-2,+∞)上存在两个不等的实根,
令p(x)=2x2+4x+a,
∴△=16-8a>0且p(-2)>0,
∴0<a<2,
∵x1+x2=-2,x1x2=$\frac{a}{2}$,
∴g(x1)+g(x2)=x12+aln(x1+2)+x22+aln(x2+2)
=(x1+x2)2-2x1x2+aln[x1x2+2(x1+x2)+4]=aln$\frac{a}{2}$-a+4
令q(x)=xln$\frac{x}{2}$-x+4,x∈(0,2),
∴q′(x)=ln$\frac{x}{2}$<0,
∴q(x)在(0,2)上单调递减,
∴2<aln$\frac{a}{2}$-a+4,
∴g(x1)+g(x2)>2.
点评 本题考查导数知识的运用,考查韦达定理,考查函数的单调性与极值,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
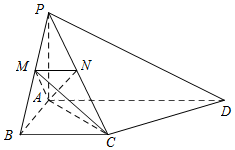 如图,PA⊥平面ABCD,AB⊥AD,AD∥BC,PA=AB=BC,AD=2AB,点M,N分别在PB,PC上,且MN∥BC.
如图,PA⊥平面ABCD,AB⊥AD,AD∥BC,PA=AB=BC,AD=2AB,点M,N分别在PB,PC上,且MN∥BC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{{2}^{k}+1}$ | B. | $\frac{1}{{2}^{k+1}}$ | ||
| C. | $\frac{1}{{2}^{k}+1}$+$\frac{1}{{2}^{k}+2}$+…+$\frac{1}{{2}^{k+1}}$ | D. | $\frac{1}{{2}^{k}}$+$\frac{1}{{2}^{k}+1}$+…+$\frac{1}{{2}^{k+1}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{3}$个单位长度 | B. | 向右平移$\frac{π}{3}$个单位长度 | ||
| C. | 向左平移$\frac{2π}{3}$个单位长度 | D. | 向右平移$\frac{2π}{3}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x3 | B. | y=cosx | C. | y=ln$\frac{1-x}{1+x}$ | D. | y=ex |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com