
| A. | 若该大学某女生身高为170cm,则她的体重必为58.79kg | |
| B. | y与x具有正的线性相关关系 | |
| C. | 回归直线过样本点的中心($\overline x$,$\overline y$) | |
| D. | 身高x为解释变量,体重y为预报变量 |
分析 根据回归方程$\stackrel{∧}{y}$=0.85x-85.71及其意义,对选项中的命题进行分析、判断即可.
解答 解:回归方程$\stackrel{∧}{y}$=0.85x-85.71中,
当x=170cm时,$\stackrel{∧}{y}$=0.85×170-85.71=58.79kg,
即大学某女生身高为170cm,她的体重应在58.79kg左右,A不正确;
$\stackrel{∧}{b}$=0.85>0,是正相关,B正确;
回归直线过样本点的中心($\overline x$,$\overline y$),C正确;
身高x为解释变量,体重y为预报变量,D正确.
故选:A.
点评 本题考查了回归方程的意义与应用问题,是基础题目.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:填空题
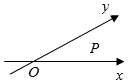 如图,当∠xOy=α,且α∈(0,$\frac{π}{2}$)∪($\frac{π}{2}$,π)时,定义平面坐标系xOy为α-仿射坐标系.在α-仿射坐标系中,任意一点P的斜坐标这样定义:$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$分别为与x轴、y轴正向相同的单位向量,若$\overrightarrow{OP}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$,则记为$\overrightarrow{OP}$=(x,y).现给出以下说法:
如图,当∠xOy=α,且α∈(0,$\frac{π}{2}$)∪($\frac{π}{2}$,π)时,定义平面坐标系xOy为α-仿射坐标系.在α-仿射坐标系中,任意一点P的斜坐标这样定义:$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$分别为与x轴、y轴正向相同的单位向量,若$\overrightarrow{OP}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$,则记为$\overrightarrow{OP}$=(x,y).现给出以下说法:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{{2}^{k}+1}$ | B. | $\frac{1}{{2}^{k+1}}$ | ||
| C. | $\frac{1}{{2}^{k}+1}$+$\frac{1}{{2}^{k}+2}$+…+$\frac{1}{{2}^{k+1}}$ | D. | $\frac{1}{{2}^{k}}$+$\frac{1}{{2}^{k}+1}$+…+$\frac{1}{{2}^{k+1}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{3}$个单位长度 | B. | 向右平移$\frac{π}{3}$个单位长度 | ||
| C. | 向左平移$\frac{2π}{3}$个单位长度 | D. | 向右平移$\frac{2π}{3}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com