
分析 (1)求出函数的导数,根据f(x0)=0,f′(x0)=0,求出a的值即可;
(2)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,通过讨论求出函数的最小值即可.
解答 解:(1)∵f(x)=lnx-ax,(a∈R,x>0)
∴f′(x)=$\frac{1}{x}$-a,
设切点为(x0,0),
则$\left\{{\begin{array}{l}{f'({x_0})=0}\\{f({x_0})=0}\end{array}}\right.$,故$\left\{{\begin{array}{l}{\frac{1}{x_0}-a=0}\\{ln{x_0}-a{x_0}=0}\end{array}}\right.$,
解得$a=\frac{1}{e}$.┅┅4分
(2)$由f(x)=lnx-ax得f'(x)=\frac{1}{x}-a=\frac{-ax+1}{x}$,
∵x>0,a>0,
$令f'(x)>0得0<x<\frac{1}{a}$;$令f'(x)<0得x>\frac{1}{a}$,
∴f(x)在(0,$\frac{1}{a}$)递增,在($\frac{1}{a}$,+∞)递减;
①当$\frac{1}{a}$≤1,即a≥1时,函数f(x)在区间[1,2]上是减函数,
∴f(x)的最小值是f(2)=ln2-2a.
②当$\frac{1}{a}$≥2,即$0<a≤\frac{1}{2}$时,函数f(x)在区间[1,2]上是增函数,
∴f(x)的最小值是f(1)=-a.┅┅7分
③当1<$\frac{1}{a}$<2,即$\frac{1}{2}$<a<1时,函数f(x)在[1,$\frac{1}{a}$]上是增函数,在[$\frac{1}{a}$,2]是减函数.
又f(2)-f(1)=ln2-a,┅┅9分
∴当$\frac{1}{2}$<a<ln2时,最小值是f(1)=-a;
当ln2≤a<1时,最小值为f(2)=ln2-2a.
综上可知,当0<a<ln2时,函数f(x)的最小值是f(x)min=-a;
当a≥ln2时,函数f(x)的最小值是f(x)min=ln2-2a.
点评 本题考查了函数的单调性、最值问题,考查导数的应用,是一道中档题.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 若该大学某女生身高为170cm,则她的体重必为58.79kg | |
| B. | y与x具有正的线性相关关系 | |
| C. | 回归直线过样本点的中心($\overline x$,$\overline y$) | |
| D. | 身高x为解释变量,体重y为预报变量 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+2 | B. | 1+2+3+4 | C. | 1+2+3 | D. | 1+2+3+4+5+6+7+8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①④ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{3}$ | B. | -35 | C. | 35 | D. | -$\frac{7}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
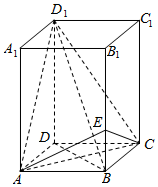 已知长方体AC1中,棱AB=BC=1,棱BB1=2,点E为棱BB1上的点.
已知长方体AC1中,棱AB=BC=1,棱BB1=2,点E为棱BB1上的点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com