
分析 ①求出复数在第三象限的等价条件,结合充分条件和必要条件的定义进行判断,
②根据线面垂直和面面垂直的关系进行判断
③根据对数和指数幂的大小关系进行判断
④根据抛物线的定义和性质进行判断.
解答 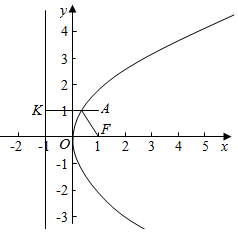 解:①复数z=$\frac{3-ai}{i}$=-a-3i,在复平面内对应的点在第三象限,则等价为-a<0,则a>0,
解:①复数z=$\frac{3-ai}{i}$=-a-3i,在复平面内对应的点在第三象限,则等价为-a<0,则a>0,
则a>0是a≥0的充分不必要条件;故①正确,
②因为直线l?α,且l⊥β,所以由判断定理得α⊥β.
所以直线l?α,且l⊥β⇒α⊥β
若α⊥β,直线l?α则直线l⊥β,或直线l∥β,或直线l与平面β相交,或直线l在平面β内.
所以“l⊥β”是“α⊥β”成立的充分不必要条件;故②错误,
③$a={log_{\frac{1}{3}}}2$=-log32∈(-1,0),b=log${\;}_{\frac{1}{2}}$3=-log23<-1,$c={(\frac{1}{3})^{0.5}}$>0,
∴b<a<c;故③错误,
④因为点A在抛物线开口之内,所以过A向抛物线的准线x=-1作垂线AK,垂足为K,交抛物线于点P,连接PF,则P即为所求.由抛物线的定义可知PF=PK,AK=AP+PK=AP+PF=2,由三点共线知识可得此时PA+PF最小,故④正确,
故答案为:①④
点评 本题主要考查命题的真假判断,涉及的知识点较多,综合性较强,有一定的难度.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知抛物线C1:y2=4x的焦点为F,椭圆C2的中心在原点,F为其右焦点,点M为曲线C1和C2在第一象限的交点,且|$\overrightarrow{MF}$|=$\frac{5}{2}$.
如图,已知抛物线C1:y2=4x的焦点为F,椭圆C2的中心在原点,F为其右焦点,点M为曲线C1和C2在第一象限的交点,且|$\overrightarrow{MF}$|=$\frac{5}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
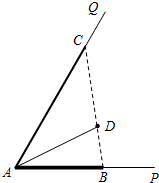 如图所示,∠PAQ是村里一个小湖的一角,其中∠PAQ=60°.为了给村民营造丰富的休闲环境,村委会决定在直线湖岸AP与AQ上分别建观光长廊AB与AC,其中AB是宽长廊,造价是800元/米;AC是窄长廊,造价是400元/米;两段长廊的总造价预算为12万元(恰好都用完);同时,在线段BC上靠近点B的三等分点D处建一个表演舞台,并建水上通道AD(表演舞台的大小忽略不计),水上通道的造价是600元/米.
如图所示,∠PAQ是村里一个小湖的一角,其中∠PAQ=60°.为了给村民营造丰富的休闲环境,村委会决定在直线湖岸AP与AQ上分别建观光长廊AB与AC,其中AB是宽长廊,造价是800元/米;AC是窄长廊,造价是400元/米;两段长廊的总造价预算为12万元(恰好都用完);同时,在线段BC上靠近点B的三等分点D处建一个表演舞台,并建水上通道AD(表演舞台的大小忽略不计),水上通道的造价是600元/米.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
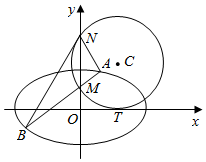 如图,圆C与x轴相切于点T(2,0),与y轴正半轴相交于两点M,N(点M在点N的下方),且|MN|=3.
如图,圆C与x轴相切于点T(2,0),与y轴正半轴相交于两点M,N(点M在点N的下方),且|MN|=3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
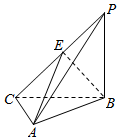 如图,三棱锥P-ABC中,PB⊥平面ABC,PB=BC=CA=4,∠BCA=90°,E为PC的中点.
如图,三棱锥P-ABC中,PB⊥平面ABC,PB=BC=CA=4,∠BCA=90°,E为PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com