
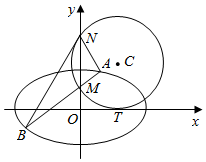
 如图,圆C与x轴相切于点T(2,0),与y轴正半轴相交于两点M,N(点M在点N的下方),且|MN|=3.
如图,圆C与x轴相切于点T(2,0),与y轴正半轴相交于两点M,N(点M在点N的下方),且|MN|=3.分析 (Ⅰ)设圆C的半径为r(r>0),依题意,圆心坐标为(2,r),根据|MN|=3,利用弦长公式求得r的值,可得圆C的方程.
(Ⅱ)把x=0代入圆C的方程,求得M、N的坐标,当AB⊥y轴时,由椭圆的对称性可知∠ANM=∠BNM,当AB与y轴不垂直时,可设直线AB的方程为y=kx+1,代入椭圆的方程,利用韦达定理求得KAB+KBN=0,可得∠ANM=∠BNM.
解答  解:(Ⅰ)设圆C的半径为r(r>0),依题意,圆心坐标为(2,r).
解:(Ⅰ)设圆C的半径为r(r>0),依题意,圆心坐标为(2,r).
∵|MN|=3,∴${r^2}={({\frac{3}{2}})^2}+{2^2}$,解得${r^2}=\frac{25}{4}$,
故圆C的方程为${({x-2})^2}+{({y-\frac{5}{2}})^2}=\frac{25}{4}$.
(Ⅱ)把x=0代入方程${({x-2})^2}+{({y-\frac{5}{2}})^2}=\frac{25}{4}$,解得y=1或y=4,
即点M(0,1),N(0,4).
(1)当AB⊥y轴时,由椭圆的对称性可知∠ANM=∠BNM.
(2)当AB与y轴不垂直时,可设直线AB的方程为y=kx+1.
联立方程$\left\{\begin{array}{l}y=kx+1\\{x^2}+2{y^2}=8\end{array}\right.$,消去y得,(1+2k2)x2+4kx-6=0.
设直线AB交椭圆Γ于A(x1,y1)、B(x2,y2)两点,
则${x_1}+{x_2}=\frac{-4k}{{1+2{k^2}}}$,${x_1}{x_2}=\frac{-6}{{1+2{k^2}}}$.
∴${k_{AN}}+{k_{BN}}=\frac{{{y_1}-4}}{x_1}+\frac{{{y_2}-4}}{x_2}=\frac{{k{x_1}-3}}{x_1}+\frac{{k{x_2}-3}}{x_2}=\frac{{2k{x_1}{x_2}-3({x_1}+{x_2})}}{{{x_1}{x_2}}}$=0,
∴∠ANM=∠BNM.
综上所述,∠ANM=∠BNM.
点评 本题考查了圆的标准方程求法以及圆锥曲线问题中韦达定理的应用,弦长公式,是综合类的题目,考虑到证两条直线的斜率互为相反数是解决此题的关键,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
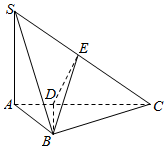 在三棱锥S-ABC中,SA⊥底面ABC,AB⊥BC,DE垂直平分SC且分别交AC、SC于D、E,又SA=AB,SB=BC,
在三棱锥S-ABC中,SA⊥底面ABC,AB⊥BC,DE垂直平分SC且分别交AC、SC于D、E,又SA=AB,SB=BC,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在直三棱柱ABC-A1B1C1中,底面△ABC是直角三角形,AB=AC=1,点P是棱BB1上一点,满足$\overrightarrow{BP}=λ\overrightarrow{B{B_1}}$(0≤λ≤1).
如图,在直三棱柱ABC-A1B1C1中,底面△ABC是直角三角形,AB=AC=1,点P是棱BB1上一点,满足$\overrightarrow{BP}=λ\overrightarrow{B{B_1}}$(0≤λ≤1).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
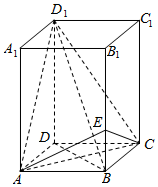 已知长方体AC1中,棱AB=BC=1,棱BB1=2,点E为棱BB1上的点.
已知长方体AC1中,棱AB=BC=1,棱BB1=2,点E为棱BB1上的点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
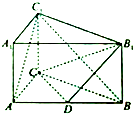 如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,AB=5,BC=4,AC=CC1=3,D为AB的中点
如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,AB=5,BC=4,AC=CC1=3,D为AB的中点查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com