
 如图,在直三棱柱ABC-A1B1C1中,底面△ABC是直角三角形,AB=AC=1,点P是棱BB1上一点,满足$\overrightarrow{BP}=λ\overrightarrow{B{B_1}}$(0≤λ≤1).
如图,在直三棱柱ABC-A1B1C1中,底面△ABC是直角三角形,AB=AC=1,点P是棱BB1上一点,满足$\overrightarrow{BP}=λ\overrightarrow{B{B_1}}$(0≤λ≤1).分析 (1)以A为坐标原点O,分别以AB,AC,AA1所在直线为x轴、y轴、z轴,建立空间直角坐标系O-xyz,利用向量法能求出直线PC与平面A1BC所成的角的正弦值.
(2)求出平面PA1C的法向量和平面PA1C的法向量,利用向量法能求出λ的值.
解答 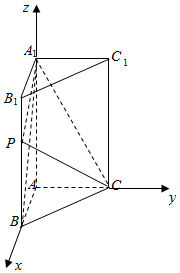 解:(1)以A为坐标原点O,分别以AB,AC,AA1所在直线为x轴、y轴、z轴,
解:(1)以A为坐标原点O,分别以AB,AC,AA1所在直线为x轴、y轴、z轴,
建立空间直角坐标系O-xyz.
∵AB=AC=1,AA1=2,则A(0,0,0),B(1,0,0),C(0,1,0),
A1(0,0,2),B1(1,0,2),P(1,0,2λ).…(1分)
由$λ=\frac{1}{3}$得,$\overrightarrow{CP}=(1,-1,\frac{2}{3})$,$\overrightarrow{{A_1}B}=(1,0,-2)$,$\overrightarrow{{A_1}C}=(0,1,-2)$,
设平面A1BC的法向量为$\overrightarrow{n}$=(x1,y1,z1),由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{{A}_{1}B}=0}\\{\overrightarrow{n}•\overrightarrow{{A}_{1}C}=0}\end{array}\right.$,得$\left\{\begin{array}{l}{x_1}-2{z_1}=0\\{y_1}-2{z_1}=0.\end{array}\right.$
取z1=1,则x1=y1=2,从而平面A1BC的一个法向量为$\overrightarrow{n}$=(2,2,1).…(3分)
设直线PC与平面A1BC所成的角为θ,
则sinθ=|cos<$\overrightarrow{CP},\overrightarrow{n}$>|=$\frac{|\overrightarrow{CP}•\overrightarrow{n}|}{|\overrightarrow{CP}|•|\overrightarrow{n}|}$=$\frac{\sqrt{22}}{33}$,
∴直线PC与平面A1BC所成的角的正弦值为$\frac{{\sqrt{22}}}{33}$.…(5分)
(2)设平面PA1C的法向量为$\overrightarrow{m}$=(x2,y2,z2),$\overrightarrow{{A_1}P}=(1,0,\;2λ-2)$,
由$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{{A}_{1}C}=0}\\{\overrightarrow{m}•\overrightarrow{{A}_{1}P}=0}\end{array}\right.$,得$\left\{\begin{array}{l}{y_2}-2{z_2}=0\\{x_2}+(2λ-2){z_2}=0.\end{array}\right.$
取z2=1,则x2=2-2λ,y2=2,平面PA1C的法向量为$\overrightarrow{m}$=(2-2λ,2,1).…(7分)
则cos<$\overrightarrow{m},\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{9-4λ}{3\sqrt{4{λ}^{2}-8λ+9}}$,
又∵二面角P-A1C-B的正弦值为$\frac{2}{3}$,∴$\frac{9-4λ}{{3\sqrt{4{λ^2}-8λ+9}}}=\frac{{\sqrt{5}}}{3}$,…(9分)
化简得λ2+8λ-9=0,解得λ=1或λ=-9(舍去),
故λ的值为1. …(10分)
点评 本题考查线面角的正弦值的求法,考查实数值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | y=x3 | B. | y=cosx | C. | y=ln$\frac{1-x}{1+x}$ | D. | y=ex |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
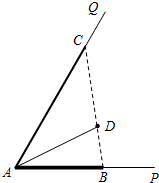 如图所示,∠PAQ是村里一个小湖的一角,其中∠PAQ=60°.为了给村民营造丰富的休闲环境,村委会决定在直线湖岸AP与AQ上分别建观光长廊AB与AC,其中AB是宽长廊,造价是800元/米;AC是窄长廊,造价是400元/米;两段长廊的总造价预算为12万元(恰好都用完);同时,在线段BC上靠近点B的三等分点D处建一个表演舞台,并建水上通道AD(表演舞台的大小忽略不计),水上通道的造价是600元/米.
如图所示,∠PAQ是村里一个小湖的一角,其中∠PAQ=60°.为了给村民营造丰富的休闲环境,村委会决定在直线湖岸AP与AQ上分别建观光长廊AB与AC,其中AB是宽长廊,造价是800元/米;AC是窄长廊,造价是400元/米;两段长廊的总造价预算为12万元(恰好都用完);同时,在线段BC上靠近点B的三等分点D处建一个表演舞台,并建水上通道AD(表演舞台的大小忽略不计),水上通道的造价是600元/米.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
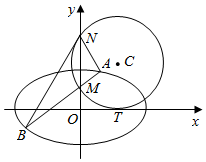 如图,圆C与x轴相切于点T(2,0),与y轴正半轴相交于两点M,N(点M在点N的下方),且|MN|=3.
如图,圆C与x轴相切于点T(2,0),与y轴正半轴相交于两点M,N(点M在点N的下方),且|MN|=3.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,二面角α-l-β的大小为60°,A∈β,C∈α,且AB、CD都垂直于棱l,分别交棱l于B、D.已知BD=1,AB=2,CD=3,则AC=2$\sqrt{2}$.
如图,二面角α-l-β的大小为60°,A∈β,C∈α,且AB、CD都垂直于棱l,分别交棱l于B、D.已知BD=1,AB=2,CD=3,则AC=2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
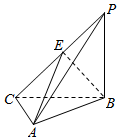 如图,三棱锥P-ABC中,PB⊥平面ABC,PB=BC=CA=4,∠BCA=90°,E为PC的中点.
如图,三棱锥P-ABC中,PB⊥平面ABC,PB=BC=CA=4,∠BCA=90°,E为PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
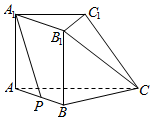 已知多面体ABC-A1B1C1中,底面△ABC为等边三角形,边长为2,AA1⊥平面ABC,四边形A1ACC1为直角梯形,CC1与平面ABC所成的角为$\frac{π}{4}$,AA1=1
已知多面体ABC-A1B1C1中,底面△ABC为等边三角形,边长为2,AA1⊥平面ABC,四边形A1ACC1为直角梯形,CC1与平面ABC所成的角为$\frac{π}{4}$,AA1=1查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
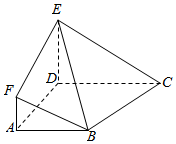 如图所示,平面四边形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AD⊥ED,AF∥DE,AB∥CD,CD=2AB=2AD=2ED=xAF.
如图所示,平面四边形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AD⊥ED,AF∥DE,AB∥CD,CD=2AB=2AD=2ED=xAF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com