
 如图,二面角α-l-β的大小为60°,A∈β,C∈α,且AB、CD都垂直于棱l,分别交棱l于B、D.已知BD=1,AB=2,CD=3,则AC=2$\sqrt{2}$.
如图,二面角α-l-β的大小为60°,A∈β,C∈α,且AB、CD都垂直于棱l,分别交棱l于B、D.已知BD=1,AB=2,CD=3,则AC=2$\sqrt{2}$. 分析 根据二面角的大小,利用向量的数量积的应用即可求AC的长度
解答 解:由题意知$\overrightarrow{AB}$⊥$\overrightarrow{BD}$,$\overrightarrow{BD}$⊥$\overrightarrow{DC}$,即$\overrightarrow{AB}$•$\overrightarrow{BD}$=0,$\overrightarrow{BD}$•$\overrightarrow{DC}$=0,<$\overrightarrow{DC}$,$\overrightarrow{BA}$>=60°,
∵$\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{BD}$+$\overrightarrow{DC}$,
∴|$\overrightarrow{AC}$|2=($\overrightarrow{AB}$+$\overrightarrow{BD}$+$\overrightarrow{DC}$)2=|$\overrightarrow{AB}$|2+|$\overrightarrow{BD}$|2+|$\overrightarrow{DC}$|2+2$\overrightarrow{AB}$•$\overrightarrow{BD}$+2$\overrightarrow{DC}$•$\overrightarrow{AB}$+2$\overrightarrow{BD}$′$\overrightarrow{DC}$=|$\overrightarrow{AB}$|2+|$\overrightarrow{BD}$|2+|$\overrightarrow{DC}$|2+2$\overrightarrow{DC}$•$\overrightarrow{AB}$,
∵BD=1,AB=2,CD=3,
∴|$\overrightarrow{AC}$|2=|$\overrightarrow{AB}$|2+|$\overrightarrow{BD}$|2+|$\overrightarrow{DC}$|2+2$\overrightarrow{DC}$•$\overrightarrow{AB}$
=4+9+1+2×3×2cos120°,
=14-6=8,
则|$\overrightarrow{CA}$|=$\sqrt{8}$=2$\sqrt{2}$,
即AC=2$\sqrt{2}$,
故答案为:2$\sqrt{2}$.
点评 本题主要考查向量数量积的应用,结合二面角的大小运用向量法是解决本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在直三棱柱ABC-A1B1C1中,底面△ABC是直角三角形,AB=AC=1,点P是棱BB1上一点,满足$\overrightarrow{BP}=λ\overrightarrow{B{B_1}}$(0≤λ≤1).
如图,在直三棱柱ABC-A1B1C1中,底面△ABC是直角三角形,AB=AC=1,点P是棱BB1上一点,满足$\overrightarrow{BP}=λ\overrightarrow{B{B_1}}$(0≤λ≤1).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
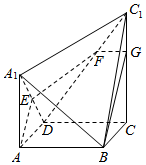 如图所示的几何体中,2CC1=3AA1=6,CC1⊥平面ABCD,且AA1⊥平面ABCD,正方形ABCD的边长为2,E为棱A1D中点,平面ABE分别与棱C1D,C1C交于点F,G.
如图所示的几何体中,2CC1=3AA1=6,CC1⊥平面ABCD,且AA1⊥平面ABCD,正方形ABCD的边长为2,E为棱A1D中点,平面ABE分别与棱C1D,C1C交于点F,G.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
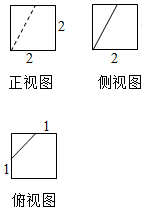 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )| A. | $\frac{47}{6}$ | B. | $\frac{15}{2}$ | C. | $\frac{23}{3}$ | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com