
分析 (1)设出点坐标,由题目条件进行计算即可;
(2)由直线EP:y=x-2,设直线CD:y=-x+t,结合圆的几何性质,解得t的值.又C,D两点均在x轴下方,直线CD:y=-x,解得C,D的坐标,进而可以解得m的值.
解答 解:(1)设曲线E上任意一点坐标为(x,y),
由题意,$\sqrt{{{(x+1)}^2}+{y^2}}=\sqrt{3}\sqrt{{{(x-1)}^2}+{y^2}}$,-----(2分)
整理得x2+y2-4x+1=0,即(x-2)2+y2=3为所求.-----(4分)
(2)由题知l1⊥l2,且两条直线均恒过点N(1,0),
设曲线E的圆心为E,则E(2,0),线段CD的中点为P,
则直线EP:y=x-2,设直线CD:y=-x+t,
由$\left\{\begin{array}{l}y=x-2\\ y=-x+t\end{array}\right.$,解得点$P(\frac{t+2}{2},\frac{t-2}{2})$,-----(6分)
由圆的几何性质,$|NP|=\frac{1}{2}|CD|=\sqrt{|ED{|^2}-|EP{|^2}}$,
而$|NP{|^2}={(\frac{t+2}{2}-1)^2}+{(\frac{t-2}{2})^2}$,|ED|2=3,$|EP{|^2}={(\frac{|2-t|}{{\sqrt{2}}})^2}$,解之得t=0或t=3,
又C,D两点均在x轴下方,直线CD:y=-x.
由$\left\{\begin{array}{l}{x^2}+{y^2}-4x+1=0\\ y=-x\end{array}\right.$解得$\left\{\begin{array}{l}x=1-\frac{{\sqrt{2}}}{2}\\ y=\frac{{\sqrt{2}}}{2}-1\end{array}\right.$或$\left\{\begin{array}{l}x=1+\frac{{\sqrt{2}}}{2}\\ y=-\frac{{\sqrt{2}}}{2}-1.\end{array}\right.$
不失一般性,设$C(1-\frac{{\sqrt{2}}}{2},\frac{{\sqrt{2}}}{2}-1),D(1+\frac{{\sqrt{2}}}{2},-\frac{{\sqrt{2}}}{2}-1)$,--(9分)
由$\left\{\begin{array}{l}{x^2}+{y^2}-4x+1=0\\ y=u(x-1)\end{array}\right.$消y得:(u2+1)x2-2(u2+2)x+u2+1=0,(1)
方程(1)的两根之积为1,所以点A的横坐标${x_A}=2+\sqrt{2}$,
又因为点$C(1-\frac{{\sqrt{2}}}{2},\frac{{\sqrt{2}}}{2}-1)$在直线l1:x-my-1=0上,解得$m=\sqrt{2}+1$,
直线${l_1}:y=(\sqrt{2}-1)(x-1)$,所以$A(2+\sqrt{2},1)$,--(11分)
同理可得,$B(2-\sqrt{2},1)$,所以线段AB的长为$2\sqrt{2}$.--(12分)
点评 本题考查求解轨迹方程的一般方法,考查学生的计算能力,属于中档题.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
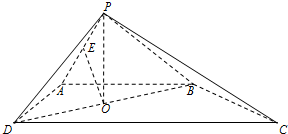
 如图,二面角α-l-β的大小为60°,A∈β,C∈α,且AB、CD都垂直于棱l,分别交棱l于B、D.已知BD=1,AB=2,CD=3,则AC=2$\sqrt{2}$.
如图,二面角α-l-β的大小为60°,A∈β,C∈α,且AB、CD都垂直于棱l,分别交棱l于B、D.已知BD=1,AB=2,CD=3,则AC=2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
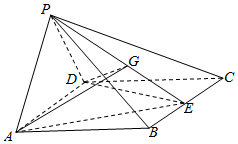 四棱锥P-ABCD中,侧面PAD⊥底面ABCD,底面ABCD是边长为2的正方形,又PA=PD,∠APD=60°,E,G分别是BC,PE的中点
四棱锥P-ABCD中,侧面PAD⊥底面ABCD,底面ABCD是边长为2的正方形,又PA=PD,∠APD=60°,E,G分别是BC,PE的中点查看答案和解析>>
科目:高中数学 来源: 题型:解答题
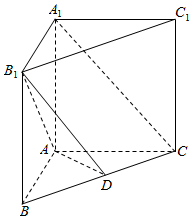 如图,直三棱柱ABC-A1B1C1中,AB=AC=2,AA1=3,D为BC中点,
如图,直三棱柱ABC-A1B1C1中,AB=AC=2,AA1=3,D为BC中点,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
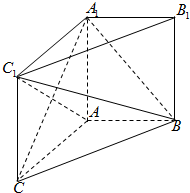 如图,在直三棱柱ABC-A1B1C1中,AC=AA1=4,AB=3,AB⊥AC.
如图,在直三棱柱ABC-A1B1C1中,AC=AA1=4,AB=3,AB⊥AC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com