
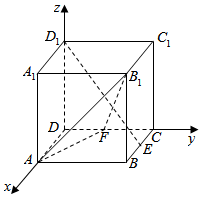
 在棱长为1的正方体ABCDA1B1C1D1中,E为棱BC的中点,点F是棱CD上的动点,试确定点F的位置,使得D1E⊥平面AB1F.
在棱长为1的正方体ABCDA1B1C1D1中,E为棱BC的中点,点F是棱CD上的动点,试确定点F的位置,使得D1E⊥平面AB1F. 分析 建立空间直角坐标系,表示出直线D1E所在的向量与AF,AB1所在的向量,利用线面垂直关系得到向量的数量积为0,进而得到答案.
解答 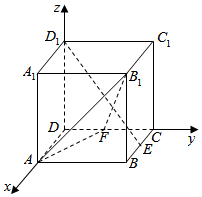 (本小题满分12分)
(本小题满分12分)
解:如图建立空间直角坐标系:
则A(1,0,0),B1(1,1,1),
D1(0,0,1),E($\frac{1}{2}$,1,0).
设F(0,y,0),则$\overrightarrow{A{B}_{1}}$=(0,1,1),
$\overrightarrow{AF}$=(-1,y,0),$\overrightarrow{{D}_{1}E}$=($\frac{1}{2}$,1,-1),
要使D1E⊥平面AB1F,
只需:$\left\{\begin{array}{l}{\overrightarrow{{D}_{1}E}•\overrightarrow{A{B}_{1}}=0}\\{\overrightarrow{{D}_{1}E}•\overrightarrow{AF}=0}\end{array}\right.$,
即:$\left\{\begin{array}{l}{1-1=0}\\{-\frac{1}{2}+y=0}\end{array}\right.$,
即:y=$\frac{1}{2}$.
∴当F为CD中点时,有D1E⊥平面AB1F.
点评 解决此类问题的常用方法是,熟悉几何体的结构特征,通过建立空间直角坐标系进而利用空间向量即可解决线面垂直、平行关系,以及空间角与空间距离等问题,本题属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 认为“选修文理科和性别有关”出错的可能性不超过5% | |
| B. | 认为“选修文理科和性别有关”出错的可能性为2.5% | |
| C. | 选修文理科和性别有95%的关系 | |
| D. | 有97.5%的把握认为“选修文理科和性别有关” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{25}$ | B. | -$\frac{7}{25}$ | C. | 1 | D. | $\frac{\sqrt{7}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 价格x(元/kg) | 10 | 15 | 20 | 25 | 30 |
| 日需求量y(kg) | 11 | 10 | 8 | 6 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
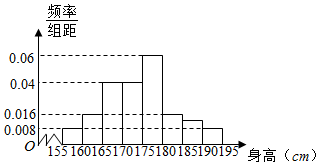 从某校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组,第一组[155,160),第二组[160,165),…,第八组[190.195],如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组人数为4.
从某校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组,第一组[155,160),第二组[160,165),…,第八组[190.195],如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组人数为4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com