
| 价格x(元/kg) | 10 | 15 | 20 | 25 | 30 |
| 日需求量y(kg) | 11 | 10 | 8 | 6 | 5 |
分析 (I)根据回归系数公式计算回归系数,得出回归方程;
(II)把x=40,代入回归方程解出y即可.
解答 解:(Ⅰ)$\overline x=\frac{1}{5}({10+15+20+25+30})=20$,(1分)
$\overline y=\frac{1}{5}({11+10+8+6+5})=8$,(2分)
$\sum_{i=1}^5{{{({{x_i}-\overline x})}^2}={{({-10})}^2}+{{({-5})}^2}+{0^2}+{5^2}+{{10}^2}=250}$,(3分)
$\sum_{i=1}^5{({{x_i}-\overline x})({{y_i}-\overline y})=}$-10×3+(-5)×2+0×0+5×(-2)+10×(-3)=-80.(4分)
$b=\frac{{\sum_{i=1}^5{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^5{{{({{x_i}-\overline x})}^2}}}}=\frac{-80}{250}=-0.32$.(6分)$a=\overline y-b\overline x=8+0.32×20=14.4$.(8分)
所求线性回归方程为$\widehaty=-0.32x+14.4$.(9分)
(Ⅱ)由(Ⅰ)知当x=40时,$\widehaty=-0.32×40+14.4=1.6$.(11分)
故当价格x=40元/kg时,日需求量y的预测值为1.6kg.(12分)
点评 本题考查线性回归方程,解题的关键是利用最小二乘法写出线性回归系数,注意解题的运算过程不要出错,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
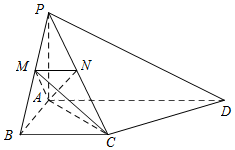 如图,PA⊥平面ABCD,AB⊥AD,AD∥BC,PA=AB=BC,AD=2AB,点M,N分别在PB,PC上,且MN∥BC.
如图,PA⊥平面ABCD,AB⊥AD,AD∥BC,PA=AB=BC,AD=2AB,点M,N分别在PB,PC上,且MN∥BC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com